Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
+ Hai cái này thực chất là 1. Chỉ khác cách tiếp cận
Hệ số góc a nói trên khía cạnh hình học. $a$ trong này có liên quan đến góc nên nó được gọi là hệ số góc của "đường thẳng" $y=ax+b$
Còn hệ số a nói trên góc độ phương trình, như em đã học ở lớp 8, nó là hệ số gắn với $x$ trong phương trình $y=ax+b$
+ Có 4 góc, nhưng ta quy ước chỉ lấy góc cắt với trục Ox ở phía trên, bên phải, tức là ở góc phần tư thứ nhất ấy.
+ Lấy ở số 1 mà không lấy ở số 0 là sao em? Khi ta vẽ điểm $(0;1)$ thì từ trục $Ox$ em lấy giá trị $x=1$, từ trục $Oy$ em lấy giá trị $y=0$ rồi dóng thẳng hai giá trị ấy để tìm điểm $A$.

a:
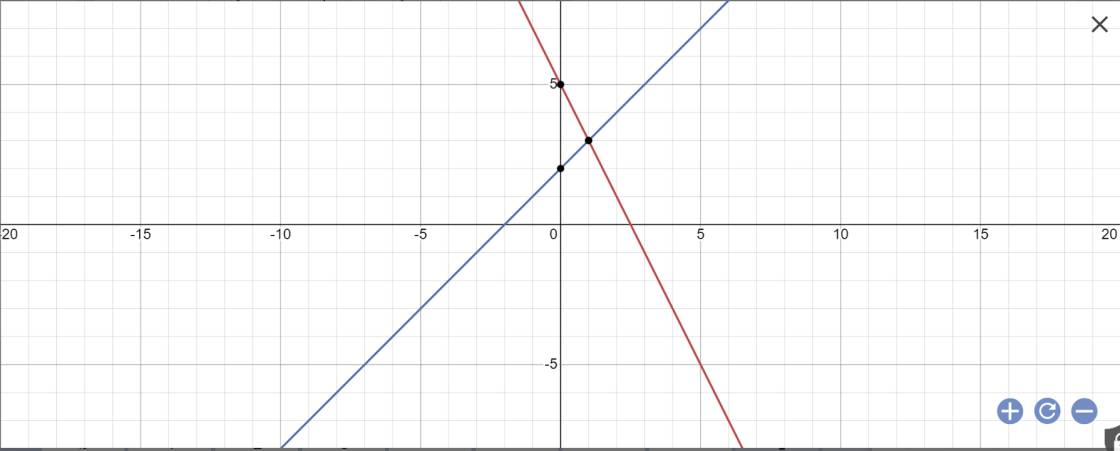
b: Phương trình hoành độ giao điểm là:
-2x+5=x+2
=>-2x-x=2-5
=>-3x=-3
=>x=1
Thay x=1 vào y=x+2, ta được;
y=1+2=3
Vậy: A(1;3)
c: Sửa đề: Tính góc tạo bởi đường thẳng y=x+2 với trục Ox
Gọi \(\alpha\) là góc tạo bởi đường thẳng y=x+2 với trục Ox
y=x+2 nên a=1
=>\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
d: Vì (d)//y=-3x-1 nên \(\left\{{}\begin{matrix}a=-3\\b\ne-1\end{matrix}\right.\)
Vậy: (d): y=-3x+b
Thay x=1 và y=3 vào (d), ta được:
\(b-3\cdot1=3\)
=>b-3=3
=>b=6(nhận)
Vậy: (d): y=-3x+6

b: Tọa độ A là:
y=0 và 3x-1=0
=>x=1/3 và y=0
Tọa độ B là:
y=0 và 3-x=0
=>x=3 và y=0
Tọa độ C là:
3x-1=-x+3 và y=3x-1
=>x=1 và y=2
c: tan a=3
nên a=71 độ

1. Phương trình d có dạng:
\(y=2\left(x-1\right)+1\Leftrightarrow y=2x-1\)
2. Do d tạo chiều dương trục Ox một góc 30 độ nên d có hệ số góc \(k=tan30^0=\dfrac{\sqrt{3}}{3}\)
Phương trình d:
\(y=\dfrac{\sqrt{3}}{3}\left(x-1\right)+2\Leftrightarrow y=\dfrac{\sqrt{3}}{3}x+\dfrac{6-\sqrt{3}}{3}\)
3. Do d tạo với trục Ox một góc 45 độ nên có hệ số góc thỏa mãn:
\(\left|k\right|=tan45^0\Rightarrow\left[{}\begin{matrix}k=1\\k=-1\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}y=1\left(x-3\right)+4\\y=-1\left(x-3\right)+4\end{matrix}\right.\)
