
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, (452 - 2.40.45 + 402) - 152
= ( 45 - 40 )2 - 152
= 52 - 152 = ( 5 - 15 )( 5 + 15 )
= -200
b, 13 . 4 . 13 .11 - 13 . 4 . 13 . 3 - 32
= 132 . 44 - 132 . 12 - 32
= 132 ( 44 -12 ) - 32
= 32 ( 132 - 1 )
= 32 . ( 13 - 1 )( 13 + 1 )
= 32 . 12 . 14
= 5376
\(45^2+40^2-15^2-80\cdot45\)
\(=\left(45^2-2\cdot45\cdot40+40^2\right)-15^2\)
\(=\left(45-40\right)^2-15^2\)
\(=15^2-15^2\)
\(=0\)
\(52\cdot143 -52\cdot39-8\cdot4\)
\(=7436-2028-32\)
\(=5408-32\)
\(=5440\)

=\(\left(2-1\right)\left(2+1\right)\left(2^2-1\right)....\left(2^{20}-1\right)\) +1
=\(\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{20}+1\right)+1\)
=\(\left(2^4-1\right)\left(2^4+1\right)....\left(2^{20}+1\right)+1\)
=.....
=\(\left(2^{20}-1\right)\left(2^{20}+1\right)+1\)
=\(2^{40}-1+1\)
=\(2^{40}\)
Chuc ban hoc tot
Sai rồi, nếu mũ là 32 thì bài này làm thế đc chứ mũ 20 thì ko làm như này được

chỗ 1994 tách riêng ra ngoài chứ ko có ngoặc đâu nha, như thế này nè:
D = (x + 1 ). ( x2 - x + 1) + x - (x - 1) . (x2 + x + 1) +1994
bạn tham khảo ở đây:
http://olm.vn/hoi-dap/question/597391.html (bài này mình vừa làm hồi nãy)
Ta có: D=x+1995
Thay x=-1995
=>D=-1995+1996=1
D=(x+1)(x2-x+1)+x-(x-1)(x2+x+1+1994) tại x=-1995
Thay x=-1995 vào đẳng thức D
D=(-1995+1)((-1995)2-(-1995)+1)+(-1995)-(-1995-1)((-1995)2+(-1995)+1+1994)
D=3978031

\(\left(c^2+b^2-5\right)^2-4\left(ab+2\right)^2\)
\(=\left(a^2+b^2-5-2ab-4\right)\left(a^2+b^2-5+2ab+4\right)\)
\(=\left(a^2+b^2-2ab-9\right)\left(a^2+b^2+2ab-1\right)\)
\(=\left[\left(a-b\right)^2-9\right]\left[\left(a+b\right)^2-1\right]\)
\(=\left(a-b-3\right)\left(a-b+3\right)\left(a+b-1\right)\left(a+b+1\right)\)

\(\left(2x^m+7y^n\right)^2=4x^{2m}+28x^my^n+49y^{2n}\)
\(\left[\left(x-3\right)-z\right]^2=\left(x-3\right)^2-2\left(x-3\right)z+z^2=x^2-6x+9-2xz+6z+z^2\)
\(\left(4a^2-3b^2\right)\left(3b^2+4a^2\right)=\left(4a^2\right)^2-\left(3b^2\right)^2=16a^4-9b^4\)
Tham khảo nhé~

\(4x^2-4\)
\(=4\left(x^2-1\right)\)
\(=4\left(x-1\right)\left(x+1\right)\)

\(\left(a^2-1\right)\left(a^2-a+1\right)\left(a^2+a+1\right)=\left(a-1\right)\left(a^2+a+1\right)\left(a+1\right)\left(a^2-a+1\right)\)
\(=\left(a^3-1\right)\left(a^3+1\right)=a^6-1\)
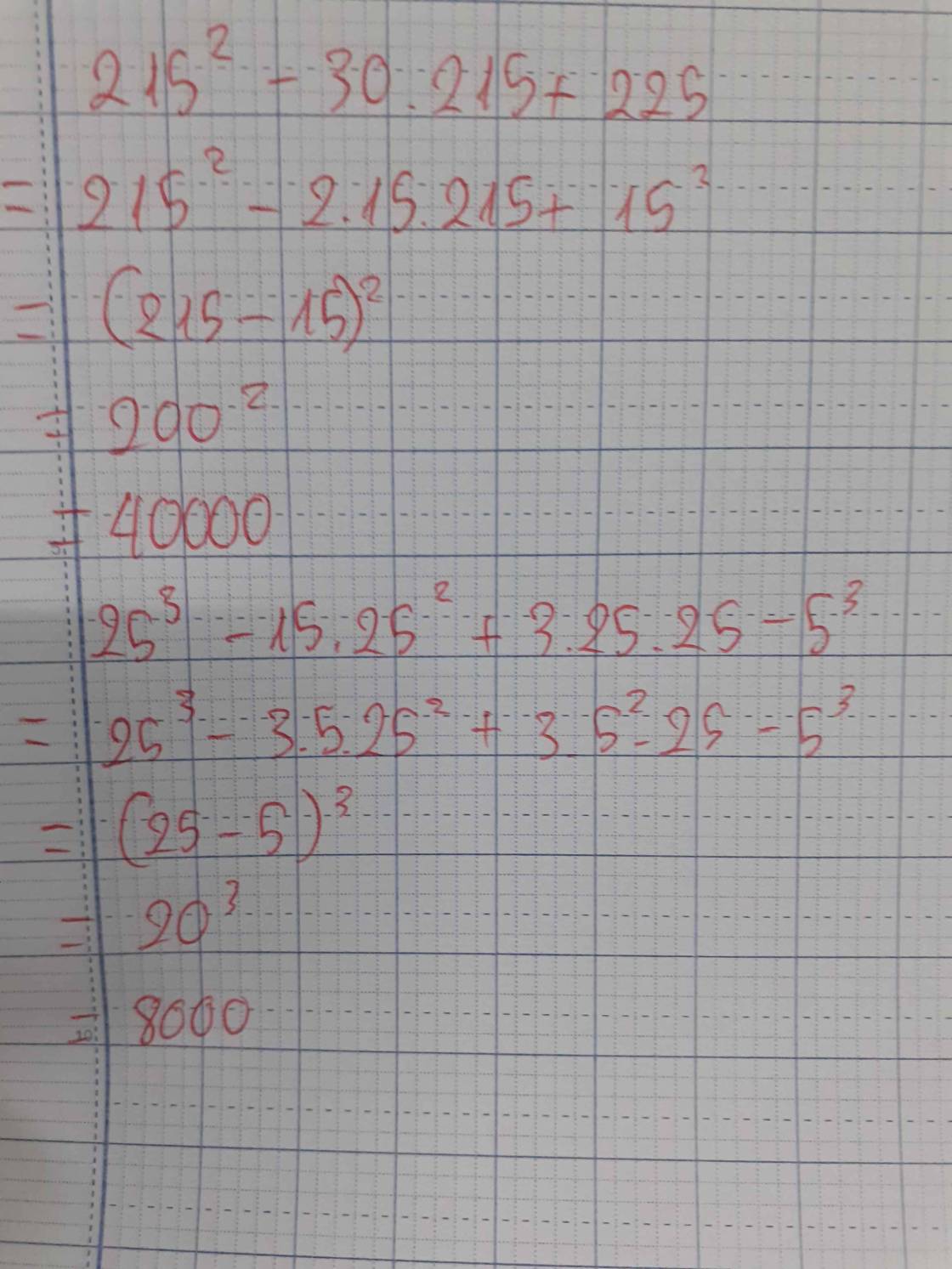
62 . 58 = (60 + 2)(60 - 2) = 60\(^2\) - 2\(^2\) = 3600 - 4 = 3596
199\(^2\) = (200 -1)\(^2\) = 200\(^2\) - 2.200.1 + 1\(^2\) = 40 000 - 400 + 1 = 39601
499\(^2\) = (500 - 1)\(^2\) = 500\(^2\) - 2.500.1 + 1\(^2\) = 250 000 - 1000 + 1 = 249 001
299 . 301 = (300 - 1)(300 + 1) = 300\(^2\) - 1\(^2\) = 90 000 - 1 = 89 999
Học tốt
Đúng thì k cho mk nhé
Trả lời:
+, \(62.58=\left(60+2\right)\left(60-2\right)=60^2-2^2=3600-4=3596\)
+, \(199^2=\left(200-1\right)^2=200^2-2.200.1+1^2=40000-400+1=39601\)
+, \(499^2=\left(500-1\right)^2=500^2-2.500.1+1^2=250000-1000+1=249001\)
+, \(299.301=\left(300-1\right)\left(300+1\right)=300^2-1=90000-1=89999\)