KA
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 12 2023
Bài 3:
a: (d1): y=2x+1; (d2): y=x+1
Vì \(a_1=2>1=a_2\)
nên (d1) cắt (d2)
b:
Bảng giá trị:
| x | -1 | 0 | 1 |
| y=2x+1 | -1 | 1 | 3 |
| y=x+1 | 0 | 1 | 2 |
Vẽ đồ thị:
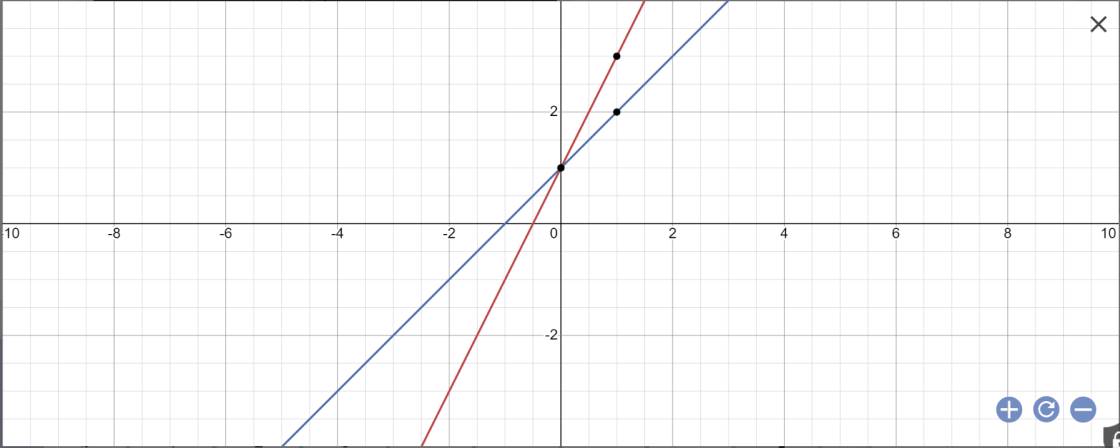
Từ đồ thị, ta sẽ thấy: (d1) cắt (d2) tại một điểm trên trục tung có tung độ bằng 1
=>(d1) cắt (d2) tại A(0;1)
c: Vì (d)//y=-4x+1 nên \(\left\{{}\begin{matrix}a=-4\\b\ne1\end{matrix}\right.\)
vậy: (d): y=-4x+b
Thay x=0 và y=1 vào (d), ta được:
\(b-4\cdot0=1\)
=>b-0=1
=>(d): y=-4x+1
d: Vì (d')//y=1/2x+9 nên \(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b\ne9\end{matrix}\right.\)
vậy: (d'): \(y=\dfrac{1}{2}x+b\)
Thay x=0 và y=1 vào (d'), ta được:
\(b+\dfrac{1}{2}\cdot0=1\)
=>b+0=1
=>b=1
Vậy: (d'): \(y=\dfrac{1}{2}x+1\)
29 tháng 6 2018
Gọi H là giao DB và EF
Có BF=BC=AD và BE=AB
Ta có: ˆEBF+ˆABC=180∘EBF^+ABC^=180∘
ˆBAD+ˆABC=180∘BAD^+ABC^=180∘
⇒ˆEBF=ˆBAD⇒EBF^=BAD^
ΔBAD=ΔEBF(c.g.c)ΔBAD=ΔEBF(c.g.c)
⇒ˆBEF=ˆABD⇒ˆBEF+ˆEBH=ˆABD+ˆEBH⇒ˆBEF+ˆEBH=90∘⇒ˆEHB=90∘⇒BEF^=ABD^⇒BEF^+EBH^=ABD^+EBH^⇒BEF^+EBH^=90∘⇒EHB^=90∘
Suy ra DB⊥EF
Dấu ^ sửa lại thành kí hiệu góc nha :3
TA
26 tháng 4 2016
b+c/a < b+c+b/2a
<=> b+c/a + a < b+c+b/2a + a
<=> b+c+a^2/a < b+c+b + a^2/a
<=> b+c+a^2/a - (b+c+b+a^2)/a <0
<=> b+c+a^2-b-c-b-a^2/a<0
<=> -b/a <0
<=> 0 < b/a ( đpcm )
27 tháng 4 2016
Xin lỗi mình viết nhầm đề cậu CM giúp mình được không
C
27 tháng 2 2020
\(A=\left(x+\frac{1}{x}\right)^2+\left(y+\frac{1}{y}\right)^2\)
\(\ge\frac{\left(x+y+\frac{1}{x}+\frac{1}{y}\right)^2}{2}\)
\(\ge\frac{\left(x+y+\frac{4}{x+y}\right)^2}{2}\)
\(=\frac{25}{2}\)
Dấu "=" xảy ra tại x=y=1/2
YN
8 tháng 10 2021
Ta xét VT:
\(a^2\left(b-c\right)+b^2\left(c-a\right)+c^2\left(a-b\right)=a^2b-a^2c+b^2c-ab^2+ac^2-bc^2\)
Ta xét VP:
\(\left(a-b\right)\left(b-c\right)\left(a-c\right)=\left(ab-ac-b^2+bc\right)\left(a-c\right)\)
\(=a^2b-a^2c-ab^2+abc-abc+ac^2+b^2c-bc^2\)
\(=a^2b-a^2c+b^2c-ab^2+ac^2-bc^2\)
Ta thấy: VT = VP
\(\Rightarrowđpcm\)
NT
1
10 tháng 8 2020
a)
\(=\frac{8^3}{\left(-8\right)^{-5}}=\frac{8^3}{-\frac{1}{8^5}}=8^3.-\left(8\right)^5=-8^8\)
b)
\(=\frac{15x^2y^2}{5xy^2}=3x\)
b) B = \(\frac{3}{1.4}\)\(+\)\(\frac{5}{4.9}\)\(+\)\(\frac{7}{9.16}\)\(+\)\(\frac{9}{16.25}\)\(+\)\(\frac{11}{25.36}\)
\(\Rightarrow\)B\(=\) 1 \(-\)\(\frac{1}{4}\)\(+\)\(\frac{1}{4}\)\(-\)\(\frac{1}{9}\)\(+\)\(\frac{1}{9}\)\(-\)\(\frac{1}{16}\)\(+\)\(\frac{1}{16}\)\(-\)\(\frac{1}{25}\)\(+\)\(\frac{1}{25}\)\(-\)\(\frac{1}{36}\)
\(\Rightarrow\)B \(=\)1 \(-\)\(\frac{1}{36}\)
\(\Rightarrow\)B \(=\) \(\frac{35}{36}\)
Vậy B \(=\) \(\frac{35}{36}\)
k dùm mik nha
thanks bạn nhìu
chúc bạn hok tốt!!