
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 4:
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Câu 1:
\(a,=\dfrac{1}{2}+9\cdot\dfrac{1}{9}-18=\dfrac{1}{2}+1-18=-\dfrac{33}{2}\\ b,=2-1+4\cdot\dfrac{1}{4}+9\cdot\dfrac{1}{9}\cdot9=1+1+9=11\\ c,=-21,3\left(54,6+45,4\right)=-21,3\cdot100=-2130\\ d,B=\left(\dfrac{1}{16}+\dfrac{1}{2}-\dfrac{1}{16}\right):\left(\dfrac{1}{8}-\dfrac{1}{8}+1\right)=\dfrac{1}{2}:1=\dfrac{1}{2}\)

c. \(\left|\dfrac{8}{4}-\left|x-\dfrac{1}{4}\right|\right|-\dfrac{1}{2}=\dfrac{3}{4}\)
\(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{8}{4}-x+\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{8}{4}+x-\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{9}{4}-x\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{7}{4}+x\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}\dfrac{9}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\\x=\dfrac{9}{4}-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\\\left[{}\begin{matrix}\dfrac{7}{4}+x-\dfrac{1}{2}=\dfrac{3}{4}\\-\dfrac{7}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\end{matrix}\right.\\\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-3\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\\x=-3\end{matrix}\right.\)
Ở nơi x=9/4-1/2 là x-9/4-1/2 nha
a. -1,5 + 2x = 2,5
<=> 2x = 2,5 + 1,5
<=> 2x = 4
<=> x = 2
b. \(\dfrac{3}{2}\left(x+5\right)-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{3}{2}x+\dfrac{15}{2}-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{9x}{6}+\dfrac{45}{6}-\dfrac{3}{6}=\dfrac{8}{6}\)
<=> 9x + 45 - 3 = 8
<=> 9x = 8 + 3 - 45
<=> 9x = -34
<=> x = \(\dfrac{-34}{9}\)




A H B D C
a) Xét \(\Delta ABH,\Delta DBH\) có :
\(AH=DH\) (H là trung điểm của AD)
\(\widehat{AHB}=\widehat{DHB}\left(=90^o\right)\)
\(HB:Chung\)
=> \(\Delta ABH=\Delta DBH\) (2 cạnh góc vuông)
=> \(\widehat{ABH}=\widehat{DBH}\) (2 góc tương ứng)
=> BH là tia phân giác của \(\widehat{ABD}\) (đpcm)
b) Ta có : \(\left\{{}\begin{matrix}\widehat{ABH}+\widehat{ABC}=180^{^O}\\\widehat{DBH}+\widehat{DBC}=180^{^O}\end{matrix}\right.\left(Kềbù\right)\)
Lại có : \(\widehat{ABH}=\widehat{DBH}\left(cmt\right)\)
Nên : \(180^{^O}-\widehat{ABH}=180^{^O}-\widehat{DBH}\)
\(\Leftrightarrow\widehat{ABC}=\widehat{DBC}\)
Xét \(\Delta ABC,\Delta DBC\) có :
\(BA=BD\) (do \(\Delta ABH=\Delta DBH\))
\(\widehat{ABC}=\widehat{DBC}\left(cmt\right)\)
BC : Chung
=> \(\Delta ABC=\Delta DBC\left(c.g.c\right)\) (*)
=> \(\widehat{ABC}=\widehat{DBC}\) (2 góc tương ứng)
c) Từ (*) suy ra : \(AC=CD\) (2 cạnh tương ứng)
=> đpcm.
 mn giải giúp mik bài 1 và bài 2a với, mik đag cần gấp, mik cảm ơn mn nhiều
mn giải giúp mik bài 1 và bài 2a với, mik đag cần gấp, mik cảm ơn mn nhiều

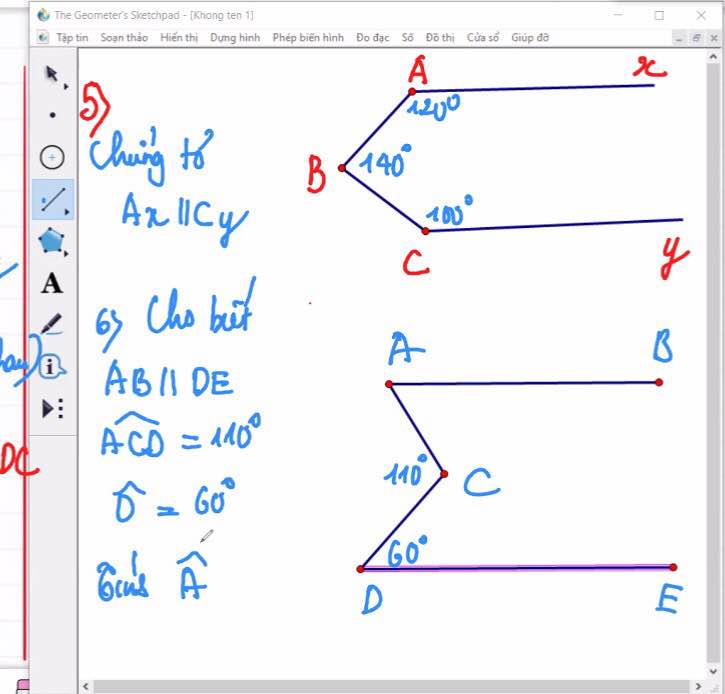
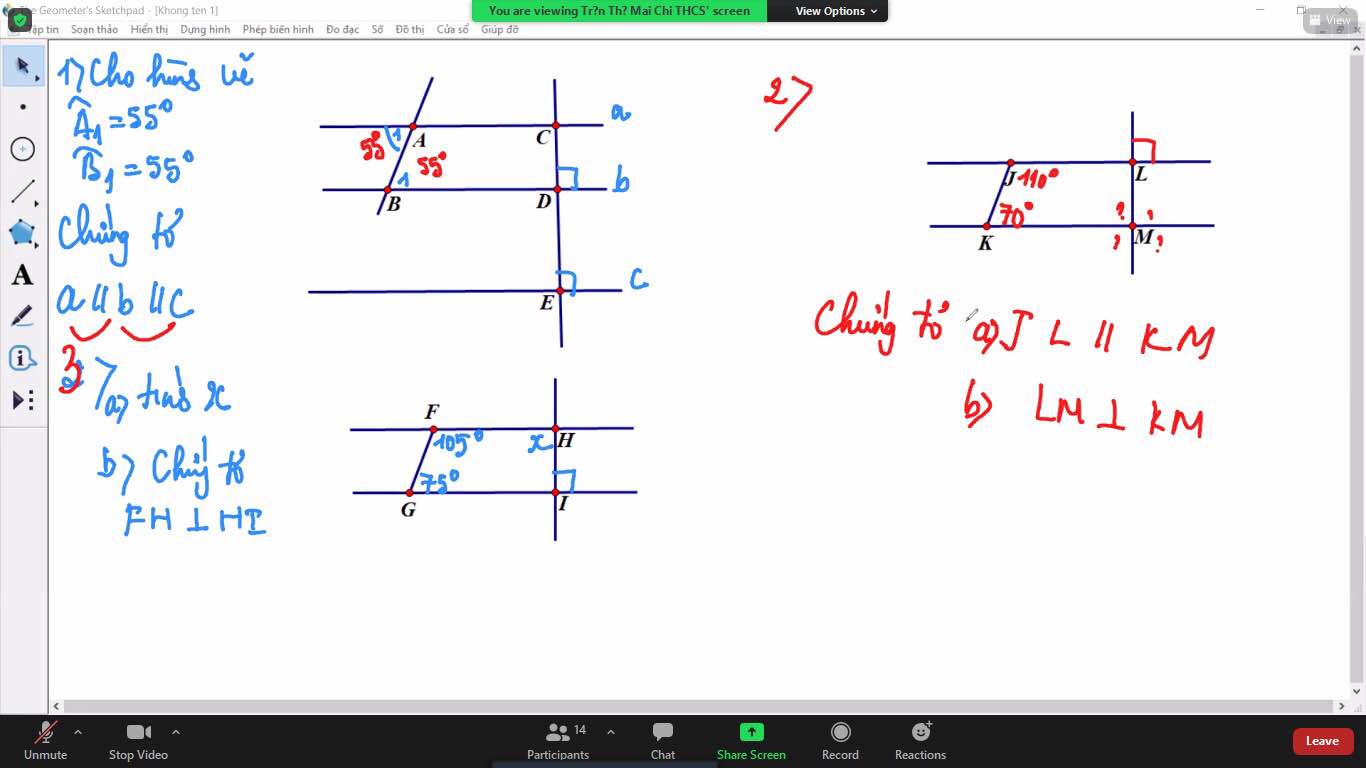

2 bài hơi nhiều đó bạn mình tách ra làm nha :))
70)
a) ΔABC cân tại A ⇒ ∠ABC = ∠ACB
⇒∠ABM = ∠ACN (vì ∠ABC + ∠ABM = ∠ACB + ∠ACN = 1800)
Xét ΔABM và ΔACN có:
AB = AC (gt); ∠ABM = ∠ACN (cmtrên); MB = NC (gt)
⇒ ΔABM = ΔACN (c.g.c)
⇒ AM = AN (Cạnh tương ứng)
⇒ ΔAMN cân tại A
b) Xét ΔHBM và ΔKCN có:
∠H = ∠K (=900)
MB = NC (gt)
∠HMB = ∠KNC (ΔAMN cân ở A)
⇒ ΔHBM = ΔKCN (Cạnh huyền – góc nhọn)
⇒ HB =KC (Cạnh tương ứng)
c) Ta có AM = AN (1) (ΔAMN cân ở A)
HM = KN (2) (ΔHBM = ΔKCN)
Từ (1) và (2) suy ra AM – HM = AN -KN hay AH = AK
d) Ta có ∠B2 = ∠C2 (ΔHBM = ΔKCN)
∠B3 = ∠B2 (Đối đỉnh)
∠C3 = ∠C2 (Đối đỉnh)
⇒ ∠B3 = ∠C3 ⇒ ΔBOC cân ở O
e)
+) ΔABC cân có ∠BAC = 600 ⇒ ΔABC đều ⇒ ∠B1 =600
Có ΔABM cân (Vì AB = BM = BC)
⇒ ∠M = ∠B1/2= 600/2 =300 (T/c góc ngoài tam giác)
⇒ ∠N = 300 (ΔAMN cận tại A)
⇒ ∠MAN = 1800 – (300 +300) = 1200
+) Xét ΔBHM có ∠H = 900, ∠M = 300 ⇒ ∠B2 =900 – ∠M = 900 – 300 =600
⇒ ∠B3 =600 (Do ∠B2 và ∠B3 đối đỉnh)
Mà ΔBOC là Δcân nên Δ BOC là Δđều.
69)
∆ABD và ∆ACD có:
AB = AC (gt)
DB = DC (gt)
AD cạnh chung.
Nên ∆ABD = ∆ACD (c.c.c)
\(\Rightarrow\) \(\widehat{A_1}=\widehat{A_2}\left(1\right)\)
Gọi H là giao điểm của AD và a.
∆AHB và ∆AHC có:
AB = AC (gt)
\(\widehat{A_1}=\widehat{A_2}\left(1\right)\)
AH cạnh chung.
Nên ∆AHB = ∆AHC (c.g.c)
Suy ra: \(\widehat{H_1}=\widehat{H_2}\)
Ta lại có: \(\widehat{H_1}+\widehat{H_2}=180^o\Rightarrow\widehat{H_1}=\widehat{H_2}=90^o\)
Vậy AD ⊥ a.