Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,2x\left(x-3\right)+5\left(x-3\right)=0\)
\(\Leftrightarrow\left(2x+5\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x+5=0\\x-3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}2x=-5\\x=3\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{5}{2}\\x=3\end{cases}}\)
Vậy .........
\(b,\left(x^2-4\right)+\left(x-2\right)\left(3-2x=0\right)\)
\(\Leftrightarrow x^2-4-2x^2+7x-6=0\)
\(\Leftrightarrow-x^2+7x-10=0\)
\(\Leftrightarrow-\left(x-5\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=5\\x=2\end{cases}}\)
Vậy ..................
\(c,x^3-3x^2+3x-1=0\)
\(\Leftrightarrow\left(x-1\right)^3=0\)
\(\Leftrightarrow x=1\)
\(d,x\left(2x-7\right)-4x+14=0\)
\(\Leftrightarrow2x^2-7x-4x+14=0\)
\(\Leftrightarrow2x^2-11x+14=0\)
\(\Leftrightarrow\left(2x-7\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{7}{2}\\x=2\end{cases}}\)
Vậy ............
\(e,\left(2x-5\right)^2-\left(x+2\right)^2=0\)
\(\Leftrightarrow4x^2-20x+25-x^2-4x-4=0\)
\(\Leftrightarrow3x^2-24x+21=0\)
\(\Leftrightarrow3\left(x-7\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-7=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=7\\x=1\end{cases}}\)
Vậy .....................
\(f,x^2-x-\left(3x-3\right)=0\)
\(\Leftrightarrow x^2-x-3x+3=0\)
\(\Leftrightarrow x^2-4x+3=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}\)
Vậy ..............

a.\(ĐKXĐ:\hept{\begin{cases}x^2-2x\ne0\\x-2\ne0\\x\left(x+1\right)\ne0\end{cases}\Leftrightarrow\hept{\begin{cases}x\left(x-2\right)\ne0\\x-2\ne0\\x\left(x+1\right)\ne0\end{cases}\Leftrightarrow}\hept{\begin{cases}x\ne0\\x\ne2\\x\ne-1\end{cases}}}\)
b.\(M=\left(\frac{1}{x^2-2x}+\frac{2}{x-2}\right)\div\frac{2x+1}{x\left(x+1\right)}\)
\(=\left(\frac{1}{x\left(x-2\right)}+\frac{2}{x-2}\right)\div\frac{2x+1}{x\left(x+1\right)}\)
\(=\left(\frac{1}{x\left(x-2\right)}+\frac{2x}{x\left(x-2\right)}\right)\div\frac{2x+1}{x\left(x+1\right)}\)
\(=\frac{2x+1}{x\left(x-2\right)}\div\frac{2x+1}{x\left(x+1\right)}\)
\(=\frac{2x+1}{x\left(x-2\right)}.\frac{x\left(x+1\right)}{2x+1}=\frac{x\left(2x+1\right)\left(x+1\right)}{x\left(x-2\right)\left(2x+1\right)}=\frac{x+1}{x-2}\)
c.Để \(M>1\)thì
\(\frac{x+1}{x-2}>1\)
c, Ta có : \(M>1\Rightarrow\frac{x+1}{x-2}>1\Leftrightarrow\frac{x+1}{x-2}-1>0\)
\(\Leftrightarrow\frac{x+1-x+2}{x-2}>0\Leftrightarrow\frac{3}{x-2}>0\)
\(\Rightarrow x-2>0\Leftrightarrow x>2\)vì 3 > 0
d, Để M nguyên khi \(x+1⋮x-2\Leftrightarrow x-2+3⋮x-2\)ĐK : \(x\ne2\)
\(\Leftrightarrow3⋮x-2\Rightarrow x-2\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
| x - 2 | 1 | -1 | 3 | -3 |
| x | 3 | 1 | 5 | -1 |

a)(2x+1)(3x-2)=(5x-8)(2x+1)
⇔(2x+1)(3x-2)-(5x-8)(2x+1)=0
⇔(2x+1)(3x-2-5x+8)=0
⇔(2x+1)(-2x+6)=0
⇔2x+1=0 hoặc -2x+6=0
1.2x+1=0⇔2x=-1⇔x=-1/2
2.-2x+6=0⇔-2x=-6⇔x=3
phương trình có 2 nghiệm x=-1/2 và x=3

a) (x-1)(5x+3)=(3x-8)(x-1)
= (x-1)(5x+3)-(3x-8)(x-1)=0
=(x-1)[(5x+3)-(3x-8)]=0
=(x-1)(5x+3-3x+8)=0
=(x-1)(2x+11)=0
\(\Leftrightarrow\) x-1=0 hoặc 2x+11=0
\(\Leftrightarrow\) x=1 hoặc x=\(\dfrac{-11}{2}\)
Vậy S={1;\(\dfrac{-11}{2}\)}
b) 3x(25x+15)-35(5x+3)=0
=3x.5(5x+3)-35(5x+3)=0
=15x(5x+3)-35(5x+3)=0
=(5x+3)(15x-35)=0
\(\Leftrightarrow\) 5x+3=0 hoặc 15x-35=0
\(\Leftrightarrow\) x=\(\dfrac{-3}{5}\) hoặc x=\(\dfrac{7}{3}\)
Vậy S={\(\dfrac{-3}{5};\dfrac{7}{3}\)}
c) (2-3x)(x+11)=(3x-2)(2-5x)
=(2-3x)(x+11)-(3x-2)(2-5x)=0
=(3x-2)[(x+11)-(2-5x)]=0
=(3x-2)(x+11-2+5x)=0
=(3x-2)(6x+9)=0
\(\Leftrightarrow\) 3x-2=0 hoặc 6x+9=0
\(\Leftrightarrow\) x=\(\dfrac{2}{3}\) hoặc x=\(\dfrac{-3}{2}\)
Vậy S={\(\dfrac{2}{3};\dfrac{-3}{2}\)}
d) (2x2+1)(4x-3)=(2x2+1)(x-12)
=(2x2+1)(4x-3)-(2x2+1)(x-12)=0
=(2x2+1)[(4x-3)-(x-12)=0
=(2x2+1)(4x-3-x+12)=0
=(2x2+1)(3x+9)=0
\(\Leftrightarrow\)2x2+1=0 hoặc 3x+9=0
\(\Leftrightarrow\)x=\(\dfrac{1}{2}\)hoặc x=\(\dfrac{-1}{2}\) hoặc x=-3
Vậy S={\(\dfrac{1}{2};\dfrac{-1}{2};-3\)}
e) (2x-1)2+(2-x)(2x-1)=0
=(2x-1)[(2x-1)+(2-x)=0
=(2x-1)(2x-1+2-x)=0
=(2x-1)(x+1)=0
\(\Leftrightarrow\) 2x-1=0 hoặc x+1=0
\(\Leftrightarrow\) x=\(\dfrac{-1}{2}\) hoặc x=-1
Vậy S={\(\dfrac{-1}{2}\);-1}
f)(x+2)(3-4x)=x2+4x+4
=(x+2)(3-4x)=(x+2)2
=(x+2)(3-4x)-(x+2)2=0
=(x+2)[(3-4x)-(x+2)]=0
=(x+2)(3-4x-x-2)=0
=(x+2)(-5x+1)=0
\(\Leftrightarrow\) x+2=0 hoặc -5x+1=0
\(\Leftrightarrow\) x=-2 hoặc x=\(\dfrac{1}{5}\)
Vậy S={-2;\(\dfrac{1}{5}\)}

a) (2x + 1)(x - 1) = 0
<=> 2x + 1 = 0 hoặc x - 1 = 0
<=> x = -1/2 hoặc x = 1
b) (x + 2/3)(x - 1/2) = 0
<=> x + 2/3 = 0 hoặc x - 1/2 = 0
<=> x = -2/3 hoặc x = 1/2
c) (3x - 1)(2x - 3)(x + 5) = 0
<=> 3x - 1 = 0 hoặc 2x - 3 = 0 hoặc x + 5 = 0
<=> x = 1/3 hoặc x = 3/2 hoặc x = -5
d) 3x - 15 = 2x(x - 5)
<=> 3x - 15 = 2x2 - 10x
<=> 3x - 15 - 2x2 + 10x = 0
<=> 13x - 15 - 2x2 = 0
<=> 2x2 - 13x + 15 = 0
<=> 2x2 - 3x - 10x + 15 = 0
<=> x(2x - 3) - 5(2x - 3) = 0
<=> (x - 5)(2x - 3) = 0
<=> x - 5 = 0 hoặc 2x - 3 = 0
<=> x = 0 hoặc x = 3/2
e) x2 - x = 0
<=> x(x - 1) = 0
<=> x = 0 hoặc x - 1 = 0
<=> x = 0 hoặc x = 1
f) x2 - 2x = 0
<=> x(x - 2) = 0
<=> x = 0 hoặc x - 2 = 0
<=> x = 0 hoặc x = 2
g) x2 - 3x = 0
<=> x(x - 3) = 0
<=> x = 0 hoặc x - 3 = 0
<=> x = 0 hoặc x = 3
h) (x + 1)(x + 2) = (2 - x)(x + 3)
<=> x2 + 2x + x + 2 = 2x + 6 - x2 - 3x
<=> x2 + 3x + 2 = -x + 6 - x2
<=> x2 + 3x + 2 + x - 6 + x2 = 0
<=> 2x2 + 4x - 4 = 0
làm nốt đi :))
nỡ giúp rùi thì bn giúp mink nốt ik vì mink ngu toán cực kì luôn
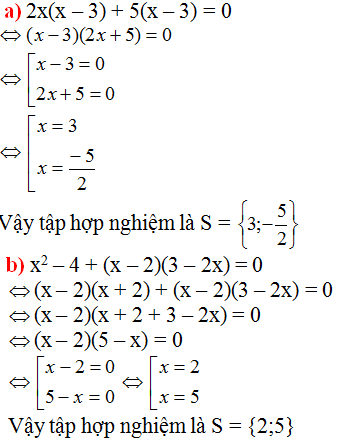
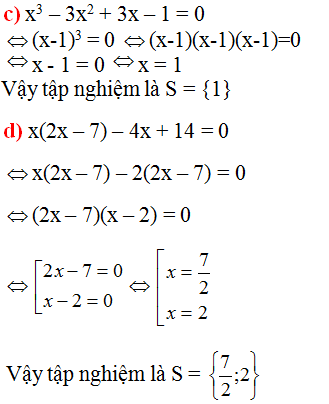
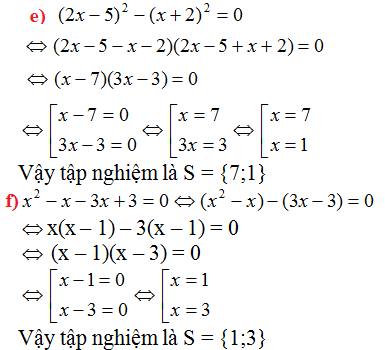

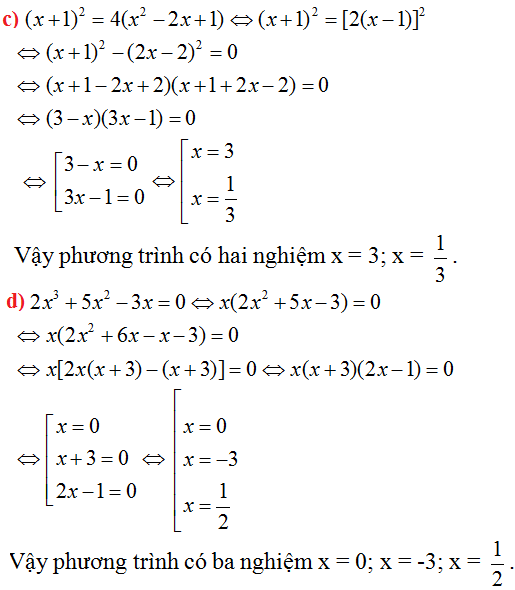
(3x + 5)2 - (2x + 1)2 = 0
<=> (3x + 5 + 2x + 1)(3x + 5 - 2x - 1) = 0
<=> (5x + 6)(x + 4) = 0
<=> \(\orbr{\begin{cases}x=-\frac{6}{5}\\x=-4\end{cases}}\)
Vậy \(x\in\left\{-\frac{6}{5};-4\right\}\)là nghiệm phương trình
\(\left(3x+5\right)^2-\left(2x+1\right)^2=0\)
\(\Leftrightarrow\left(3x+5+2x+1\right)\left(3x+5-2x-1\right)=0\)
\(\Leftrightarrow\left(5x+6\right)\left(x+4\right)=0\Leftrightarrow x=-4;x=-\frac{6}{5}\)
Vậy tập nghiệm của phương trình là S = { -4 ; -6/5 }