Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C
Ta có một năm có 365 ngày, một ngày có 24 giờ, một giờ có 60 phút và một phút có 60 giây.
Vậy một năm có 24.365.60.60 = 31536000 giây.
Vì vận tốc ánh sáng là 300 nghìn km/s nên trong vòng một năm nó đi được 31536000.300 = 9,4608.109 km.
0 km vì 1 vật có khối lượng ko thể đạt tới vận tốc ánh sáng, và chắc chắc ko có nhà khoa học nào lại nghiên cứu 1 máy bay vs tốc độ 7 lần vận tốc ánh sáng

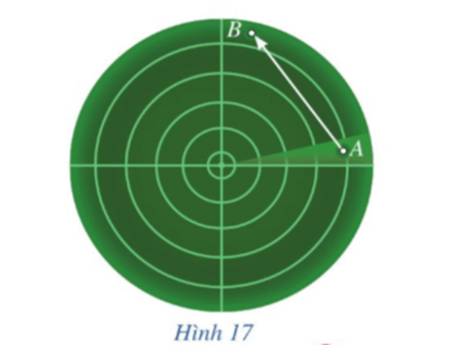
Để xác định tọa độ của máy bay trực thăng ta sử dụng biểu thức tọa độ của 2 vectơ

Để xác định tọa độ của máy bay ta phải lập phương trình quỹ đạo bay của máy bay hay chính là lập phương trình đường thẳng.

a) Vị trí máy bay vào lúc 14 giờ 30 phút là: \(\left\{ \begin{array}{l}x = \frac{{1600}}{3} - \frac{{1400}}{3}.\frac{1}{2} = 300\\y = \frac{{1900}}{3} - \frac{{1400}}{3}.\frac{1}{2} = 400\end{array} \right.\)
Vậy tọa độ máy bay là \(\left( {300;400} \right)\). Thời điểm này máy bay đã xuất hiện trên màn hình ra đa.
b) Ta có: \(MO = \sqrt {{{\left( {\frac{{1600}}{3} - \frac{{1400}}{3}t} \right)}^2} + {{\left( {\frac{{1900}}{3} - \frac{{1400}}{3}t} \right)}^2}} \).
Do có \(M{O_{\min }} = 50\sqrt 2 \Leftrightarrow t = \frac{5}{4}\).
Vậy sau khi bay \(\frac{5}{4} = 1,25\) (giờ) tức là lúc 15h15p thì máy bay gần ra đa nhất và khoảng cách từ ra đa đến máy bay khi đó là \(50\sqrt 2 \left( {km} \right)\).
c) Máy bay rời khỏi màn hình ra đa khi mà khoảng cách từ M đến O lớn hơn 500km tức là:
\(MO = \sqrt {{{\left( {\frac{{1600}}{3} - \frac{{1400}}{3}t} \right)}^2} + {{\left( {\frac{{1900}}{3} - \frac{{1400}}{3}t} \right)}^2}} \ge 500 \Leftrightarrow \left[ \begin{array}{l}t = \frac{1}{2}\\t = 2\end{array} \right.\)
Vậy sau khi bay được 2h tức là lúc 16h thì máy bay thoát khỏi màn hình ra đa.

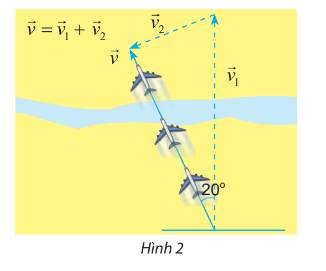
Từ giả thiết ta có:
+) Vectơ tương ứng với vận tốc máy bay là vectơ \(\overrightarrow {{v_1}} \)
+) Vectơ tương ứng với vận tốc máy bay so với mặt đất là vectơ \(\overrightarrow v \)
+) Vectơ tương ứng với vận tốc gió là vectơ \(\overrightarrow {{v_2}} \)
Ta có : \(\left| {\overrightarrow {{v_1}} } \right| = 45;\left| {\overrightarrow v } \right| = 38;\left( {\overrightarrow {{v_1}} ,\overrightarrow v } \right) = 20^\circ \)
Áp dụng định lý cosin ta có:
\(\left| {\overrightarrow {{v_2}} } \right| = \sqrt {{{\left| {\overrightarrow v } \right|}^2} + {{\left| {\overrightarrow {{v_1}} } \right|}^2} - 2\left| {\overrightarrow v } \right|.\left| {\overrightarrow {{v_1}} } \right|.\cos \left( {\overrightarrow v ,\overrightarrow {{v_1}} } \right)} \)
\( = \sqrt {{{38}^2} + {{45}^2} - 2.38.45.\cos 20^\circ } \simeq 16\) (m/s)
Vậy tốc độ của gió gần bằng 16 m/s

Tọa độ của vecto \(\overrightarrow {OM} \) là tọa độ của điểm M (trong đó O là gốc tọa độ)

a: Gọi hàm số bậc hai cần tìm là (P): \(y=ax^2+bx+c\)
Thay x=0 và y=-7 vào (P), ta được:
\(a\cdot0^2+b\cdot0+c=-7\)
=>c=-7
=>(P): \(y=ax^2+bx-7\)
Thay x=-4 và y=10 vào (P), ta được: \(a\cdot\left(-4\right)^2+b\cdot\left(-4\right)-7=10\)
=>16a-4b=17(1)
Thay x=20 và y=5 vào (P), ta được:
\(a\cdot20^2+b\cdot20-7=5\)
=>400a+20b=12(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}16a-4b=17\\400a+20b=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}80a-20b=85\\400a+20b=12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}480a=97\\16a-4b=17\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{97}{480}\\4b=16a-17=-\dfrac{413}{30}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{97}{480}\\b=-\dfrac{413}{120}\end{matrix}\right.\)
Vậy: (P): \(y=\dfrac{97}{480}x^2-\dfrac{413}{120}x-7\)

Quãng đường vật rơi được sau t(s) là: \(h(t) = 20t + \frac{1}{2}.9,8.{t^2} = 4,9.{t^2} + 20t\)
Để vật cách mặt đất không quá 100m thì \(320 - h(t) \le 100 \Leftrightarrow h(t) \ge 220 \Leftrightarrow 4,9{t^2} + 20t - 220 \ge 0 \)
Tam thức \(f(t) = 4,9{t^2} + 20t - 220\) có \(\Delta ' = 1178 > 0\) nên f(t) có 2 nghiệm phân biệt \({t_1} = \frac {- 10 - \sqrt 1178}{4,9} ;{t_2} = \frac {- 10 + \sqrt 1178}{4,9} \) (t>0)
Mặt khác a=1>0 nên ta có bảng xét dấu:

Do t > 0 nên \(t \ge \frac {- 10 + \sqrt 1178}{4,9}\approx 5 \)
Vậy sau ít nhất khoảng 5 \(s\) thì vật đó cách mặt đất không quá 100m

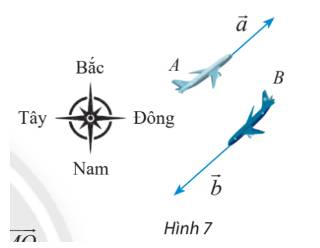
Vecto \(\overrightarrow a ,\;\overrightarrow b \) là vecto vận tốc của máy bay A và máy bay b.
Do đó \(\left| {\overrightarrow a } \right|,\;\left| {\overrightarrow b } \right|\) lần lượt là độ lớn của vecto vận tốc tương ứng.
Ta có: \(\left| {\overrightarrow a } \right| = 600,\;\left| {\overrightarrow b } \right| = 800\)
\( \Rightarrow \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{800}}{{600}} = \frac{4}{3}\)
Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó \(\overrightarrow b = - \frac{4}{3}\overrightarrow a \)
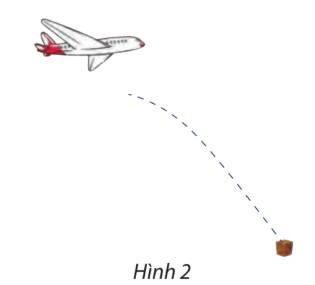


Gắn hệ trục tọa độ Oxy như hình dưới:
Gọi A vị trí hàng rơi xuống, khi đó \({y_A} = 0\). Ta có, tọa độ của A thỏa mãn:
\(\left\{ \begin{array}{l}x = 50t\\y = 80 - \frac{1}{2}.9,8.{t^2}\end{array} \right.\)
Mà \({y_A} = 0 \Rightarrow 0 = 80 - \frac{1}{2}.9,8.{t^2} \Leftrightarrow {t^2} \approx 16,33 \Rightarrow t \approx 4(s)\)
Do đó \({x_A} = 50.4 = 200(m)\) hay khoảng cách giữa máy bay và thùng hàng cứu trợ là 200m.
Vậy để thùng hàng cứu trợ rơi đúng vị trí được chọn thì máy bay cần thả hàng khi cách điểm đó 200m.