Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo định lý Pytago ta có:
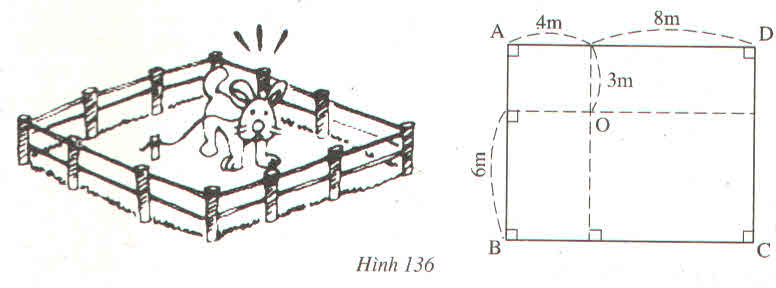
+) OA2 = 42 + 32 = 16 + 9 = 25
⇒ OA = 5m < 9m
+) OC2 = 62 + 82 = 36 + 64 = 100
⇒ OC = 10m > 9m
+) OB2 = 42 + 62 = 16 + 36 = 52
⇒ OB = √52m ≈ 7,21 (m) < 9m
+) OD2 = 32 + 82 = 9 + 64 = 73
⇒ OD = √73 ≈ 8,54(m) < 9m
Như vậy con Cún có thể tới các vị trí A, B, D nhưng không tới được vị trí C.

Ta có:
OA2=42+32
=16+9=25
Suy ra OA= 5(m)
* OC2=62+ 82=36+64=100
=> OC =10(m)
* OB2=42+62=16+26=52
=> OB=√52 ≈ 7,2(m)
* OD2=32+82=9+64=73
=>OD= √73 ≈ 8,5(m)
Nên OA=5<9; OB≈7,2<9
OC=10>9; OD≈8.5<9
Như vậy con cún có thể đi tới các vị trí A,B,D nhưng không đế được vị trí C

Áp dụng định lý Py-ta-go , ta có :
OA2 = 42 + 32 = 16 + 9 = 25
=> OA = 5
=> OA < 9
OB2 = 62 + 42 = 36 + 16 = 52
=> OB = √52
=> OB < 9
OC2 = 62 + 82 = 36 + 64 = 100
=> OC = 10
=> OC > 9
OD2 = 32 + 82 = 9 + 64 = 73
=> OD = √73
=> OD < 9
Vậy chú Cún có thể đến được các điểm A,B,D và không đến được điểm C
Bài 1 Đố: Trong lúc anh Nam dựng tủ cho đứng thẳng, tủ vướng vào trần nhà không?

Gọi x là đường chéo của tủ. h là chiều cao của nhà. h= 21dm.
Ta có x2 = 202 + 42 = 400 + 16 = 416.
=> x = √416 (1)
Và h2 =212 = 441, => h = √441 (2)
So sánh (1) và (2) ta được x < h.
Như vậy anh Nam đẩy tủ đứng thẳng không bị vướng vào trần nhà.
Bài 2 : Trên giấy kẻ ô vuông ( độ dài cạnh ô vuông bằng 1 ) , cho tam giác ABC như hình 114 . Tính độ dài mỗi cạnh của tam giác ABC .

Áp dụng định lý Py-ta-go , ta có :
AB2 = 22 + 12 = 4 + 1 = 5
=> AB = √5
AC2 = 32 + 42 = 9 + 16 = 25
=> AC = 5
BC2 = 52 + 32 = 25 + 9 = 34
=> BC = √34
Vậy ...
Gửi bn bê trần ( chúc bn hc tốt )

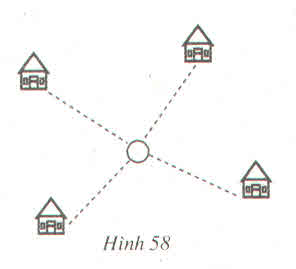
Gọi O là một điểm tùy ý (nơi phải đặt nhà máy) A, B, C, D lần lượt là bốn điểm dân cư.
Tổng khoảng cách từ nhà máy đến 4 khu dân cư là: OA + OB + OC + OD
Ta có:
Vậy khi O là giao điểm của AC và BD thì tổng khoảng cách từ nhà máy này đến các khu dân cư là ngắn nhất.
Gọi O là một điểm tùy ý (nơi phải đặt nhà máy) A, B, C, D lần lượt là bốn điểm dân cư.
Tổng khoảng cách từ nhà máy đến 4 khu dân cư là: OA + OB + OC + OD
Ta có:

Vậy khi O là giao điểm của AC và BD thì tổng khoảng cách từ nhà máy này đến các khu dân cư là ngắn nhất.

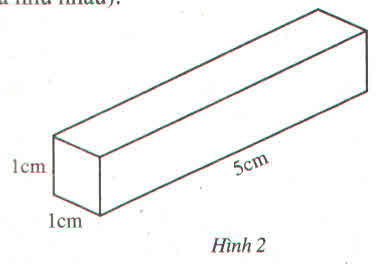
Gọi x(cm) là chiều dài của sợi dây.
Vì thể tích của khối vàng không thay đổi nên diện tích mặt cắt ngang và chiều dài hình hộp chữ nhật là hai đại lượng tỉ lệ nghịch
Ta có: \(0,01x=1.5\Rightarrow x=\dfrac{1,5}{0,01}=500\left(cm\right)\)
Vậy mặt cắt ngang là hình vuông có cạnh 1mm thì chiều dài sợi dây là 500cm.
Gọi x(cm) là chiều dài của sợi dây.
Vì thể tích của khối vàng không thay đổi nên diện tích mặt cắt ngang và chiều dài hình hộp chữ nhật là hai đại lượng tỉ lệ nghịch
Ta có: 0,01x=1.5⇒x=1,50,01=500(cm)0,01x=1.5⇒x=1,50,01=500(cm)
Vậy mặt cắt ngang là hình vuông có cạnh 1mm thì chiều dài sợi dây là 500cm.

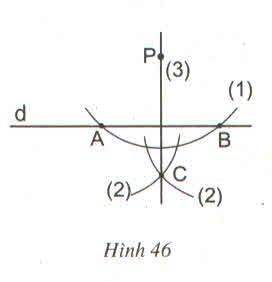
a) Ta có PA = PB (A, B nằm trên cung tròn có tâm P) CA = CB (hai cung tròn AB có tâm A và B có bán kính bằng nhau; C la giao điểm của 2 cung)
Vậy P; C cách đều A và B nên đường thẳng CP là đường trung trực của AB nên
PC ⊥ d
b) Một cách vẽ khác
- Lấy điểm A bất kì trên d
- Vẽ cung tròn tâm A bán kính AP cắt đường thẳng d tại M
- Vẽ cung tròn tâm M bán kính MP cắt cung tròn tâm A tại C
- Vẽ đường thẳng PC, đường thẳng PC chính là đường vuông góc với d.
=> PC ⊥ d (đpcm)
Hướng dẫn:
a) Ta có PA = PB (A, B nằm trên cung tròn có tâm P) CA = CB (hai cung tròn AB có tâm A và B có bán kính bằng nhau; C la giao điểm của 2 cung)
Vậy P; C cách đều A và B nên đường thẳng CP là đường trung trực của AB nên
PC ⊥ d
b) Một cách vẽ khác
- Lấy điểm A bất kì trên d
- Vẽ cung tròn tâm A bán kính AP cắt đường thẳng d tại M
- Vẽ cung tròn tâm M bán kính MP cắt cung tròn tâm A tại C
- Vẽ đường thẳng PC, đường thẳng PC chính là đường vuông góc với d.
=> PC ⊥ d (đpcm)




Ta có:
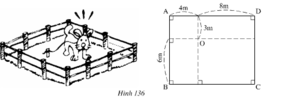
OA2=42+32
=16+9=25
Suy ra OA= 5(m)
* OC2=62+ 82=36+64=100
=> OC =10(m)
* OB2=42+62=16+26=52
=> OB=√52 ≈ 7,2(m)
* OD2=32+82=9+64=73
=>OD= √73 ≈ 8,5(m)
Nên OA=5<9; OB≈7,2<9
OC=10>9; OD≈8.5<9
Như vậy con cún có thể đi tới các vị trí A,B,D nhưng không đế được vị trí C