Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3\(\sqrt{5}\)= \(\sqrt{3^2.5}\)=\(\sqrt{45}\)
-5\(\sqrt{2}\)= \(-\sqrt{5^2.2}\)= -\(\sqrt{50}\)
\(\dfrac{-2}{3}\sqrt{xy}\) = \(-\sqrt{\left(\dfrac{2}{3}\right)^2xy}\) = -\(\sqrt{\dfrac{4}{9}xy}\)
x\(\sqrt{\dfrac{2}{x}}\)= \(\sqrt{\dfrac{2x^2}{x}}=\sqrt{2x}\)

a) Ta có : Vì \(x\ge0\)và \(y\ge0\)nên \(x+y\ge0\)\(\Leftrightarrow\left|x+y\right|=x+y\)
\(\frac{2}{x^2-y^2}\sqrt{\frac{3\left(x+y\right)^2}{2}}\)
\(=\frac{2}{x^2-y^2}\sqrt{\frac{3}{2}.\left(x+y\right)^2}\)
\(=\frac{2}{x^2-y^2}.\sqrt{\frac{3}{2}}.\left|x+y\right|\)
\(=\frac{2}{\left(x-y\right)\left(x+y\right)}.\sqrt{\frac{3}{2}}.\left(x+y\right)\)
\(=\frac{2}{x-y}.\sqrt{\frac{3}{2}}\)
\(=\frac{1}{x-y}.2.\sqrt{\frac{3}{2}}\)
\(=\frac{1}{x-y}.\sqrt{\frac{2^2.3}{2}}\)
\(=\frac{1}{x-y}.\sqrt{6}=\frac{\sqrt{6}}{x-y}\)
a, \(\frac{2}{x^2-y^2}\sqrt{\frac{3\left(x+y\right)^2}{2}}=\frac{2}{x^2-y^2}\frac{\sqrt{3}\left|x+y\right|}{\sqrt{2}}=\frac{2\sqrt{3}\left(x+y\right)}{\left(x-y\right)\left(x+y\right)\sqrt{2}}\)
do \(x\ge0;y\ge0\)
\(=\frac{2\sqrt{3}}{\sqrt{2}\left(x-y\right)}=\frac{2\sqrt{6}}{2\left(x-y\right)}=\frac{\sqrt{6}}{x-y}\)

a) a) Biến đổi vế trái thành 32√6+23√6−42√6326+236−426 và làm tiếp.
b) Biến đổi vế trái thành (√6x+13√6x+√6x):√6x(6x+136x+6x):6x và làm tiếp

+ Ta có:
2√6−√5=2(√6+√5)(√6−√5)(√6+√5)26−5=2(6+5)(6−5)(6+5)
=2(√6+√5)(√6)2−(√5)2=2(√6+√5)6−5=2(6+5)(6)2−(5)2=2(6+5)6−5
=2(√6+√5)1=2(√6+√5)=2(6+5)1=2(6+5).
+ Ta có:
3√10+√7=3(√10−√7)(√10+√7)(√10−√7)310+7=3(10−7)(10+7)(10−7)
=3(√10−√7)(√10)2−(√7)2=3(10−7)(10)2−(7)2=3(√10−√7)10−7=3(10−7)10−7
=3(√10−√7)3=√10−√7=3(10−7)3=10−7.
+ Ta có:
1√x−√y=1.(√x+√y)(√x−√y)(√x+√y)1x−y=1.(x+y)(x−y)(x+y)
=√x+√y(√x)2−(√y)2=√x+√yx−y=x+y(x)2−(y)2=x+yx−y
+ Ta có:
2ab√a−√b=2ab(√a+√b)(√a−√b)(√a+√b)2aba−b=2ab(a+b)(a−b)(a+b)
=2ab(√a+√b)(√a)2−(√b)2=2ab(√a+√b)a−b=2ab(a+b)(a)2−(b)2=2ab(a+b)a−b.
\(\frac{2}{\sqrt{6}-\sqrt{5}}=\frac{2\left(\sqrt{6}+\sqrt{5}\right)}{\left(\sqrt{6}-\sqrt{5}\right)\left(\sqrt{6}+\sqrt{5}\right)}=\frac{2\left(\sqrt{6}+\sqrt{5}\right)}{6-5}=2\left(\sqrt{6}+\sqrt{5}\right)\)
\(\frac{3}{\sqrt{10}+\sqrt{7}}=\frac{3\left(\sqrt{10}-\sqrt{7}\right)}{\left(\sqrt{10}-\sqrt{7}\right)\left(\sqrt{10}+\sqrt{7}\right)}=\frac{3\left(\sqrt{10}-\sqrt{7}\right)}{10-7}=\sqrt{10}-\sqrt{7}\)
\(\frac{1}{\sqrt{x}-\sqrt{y}}=\frac{\sqrt{x}+\sqrt{y}}{x-y}\)
\(\frac{2ab}{\sqrt{a}-\sqrt{b}}=\frac{2ab\left(\sqrt{a}+\sqrt{b}\right)}{a-b}\)

a) \(\sqrt{27x^2}=\sqrt{3.\left(3x\right)^2}=\left|3x\right|.\sqrt{3}=3x\sqrt{3}\left(x>0\right)\)
b) \(\sqrt{8xy^2}=\left|y\right|.2\sqrt{2x}=-2y\sqrt{2x}\left(x\ge0,y\le0\right)\)
1) \(x\sqrt{13}=\sqrt{13x^2}\left(x\ge0\right)\)
2) \(x\sqrt{-15x}=-\left|x\right|\sqrt{15x}=-\sqrt{15x^3}\left(x< 0\right)\)
3) \(x\sqrt{2}=-\left|x\right|\sqrt{2}=-\sqrt{2x^2}\left(x\le0\right)\)

\(3\sqrt{5}=\sqrt{45}\)
\(-5\sqrt{2}=-\sqrt{25}.\sqrt{2}=-\sqrt{50}\)
\(\dfrac{-2}{3}\sqrt{xy}=-\sqrt{\dfrac{4}{9}}.\sqrt{xy}=-\sqrt{\dfrac{4}{9}xy}\left(xy\ge0\right)\)
\(x\sqrt{\dfrac{2}{x}}=\sqrt{x^2}.\sqrt{\dfrac{2}{x}}=\sqrt{\dfrac{2x^2}{x}}=\sqrt{2x}\left(x>0\right)\)

(do xy > 0 (gt) nên đưa thừa số xy vào trong căn để khử mẫu)
#Học tốt!!!
\(ab\cdot\sqrt{\dfrac{a}{b}}=a\cdot\sqrt{ab}\)
\(\dfrac{a}{b}\cdot\sqrt{\dfrac{b}{a}}=\dfrac{\sqrt{a\cdot b}}{b}\)
\(\sqrt{\dfrac{1}{b}+\dfrac{1}{b^2}}=\dfrac{\sqrt{b+1}}{b}\)
\(\sqrt{\dfrac{9\cdot a^3}{36\cdot b}}=\dfrac{\sqrt{a^3\cdot b}}{2\cdot b}\)
\(3\cdot x\cdot y\cdot\sqrt{\dfrac{2}{x\cdot y}}=3\cdot\sqrt{2\cdot x\cdot y}\)

\(\frac{5}{\sqrt{10}}=\frac{5\sqrt{10}}{10}=\frac{\sqrt{10}}{2}\)
\(\frac{5}{2\sqrt{5}}=\frac{10\sqrt{5}}{20}=\frac{\sqrt{5}}{2}\)
\(\frac{1}{3\sqrt{20}}=\frac{3\sqrt{20}}{180}=\frac{\sqrt{20}}{60}=\frac{2\sqrt{5}}{60}=\frac{\sqrt{5}}{30}\)
\(\frac{2\sqrt{2}+2}{5\sqrt{2}}=\frac{10\sqrt{2}\left(\sqrt{2}+1\right)}{50}=\frac{20+10\sqrt{2}}{50}=\frac{10\left(2+\sqrt{2}\right)}{50}=\frac{2+\sqrt{2}}{5}\)
\(\frac{y+b\sqrt{y}}{b\sqrt{y}}=\frac{y\left(\sqrt{y}+b\right)}{by}=\frac{\sqrt{y}+b}{b}\)
+ Ta có:
5√10=5.√10√10.√10=5√10(√10)2=5√1010510=5.1010.10=510(10)2=51010
=5.√105.2=5.105.2=√102=102.
+ Ta có:
52√5=5.√52√5.√5=5√52.(√5.√5)=5√52(√5)2525=5.525.5=552.(5.5)=552(5)2
=5√52.5=√52=552.5=52.
+ Ta có:
13√20=1.√203√20.√20=√203.(√20.√20)=√203.(√20)21320=1.20320.20=203.(20.20)=203.(20)2
=√203.20=√22.560=2√560=2√52.30=√530=203.20=22.560=2560=252.30=530.
+ Ta có:
(2√2+2)5.√2=(2√2+2).√25√2.√2=2√2.√2+2.√25.(√2)2(22+2)5.2=(22+2).252.2=22.2+2.25.(2)2
=2.2+2√25.2=2(2+√2)5.2=2+√25=2.2+225.2=2(2+2)5.2=2+25.
+ Ta có:
y+b√yb√y=(y+b√y).√yb√y.√y=y√y+b√y.√yb.(√y)2y+byby=(y+by).yby.y=yy+by.yb.(y)2
=y√y+b(√y)2by=y√y+byby=yy+b(y)2by=yy+byby
=y(√y+b)b.y=√y+bb=y(y+b)b.y=y+bb.
Cách khác:
y+b√yb√y=(√y)2+b√yb√yy+byby=(y)2+byby=√y(√y+b)b√y=√y+bb
Nguồn : Bài 50 trang 30 SGK Toán 9 tập 1 - loigiaihay.com
#Ye Chi-Lien

a, \(\sqrt{\left(2x-1\right)^2}=3\Leftrightarrow\left|2x-1\right|=3\)
Với \(x\ge\frac{1}{2}\)pt có dạng : \(2x-1=3\Leftrightarrow x=2\)( tm )
Với \(x< \frac{1}{2}\)pt có dạng : \(-2x+1=3\Leftrightarrow x=-1\)( tm )
Vậy tập nghiệm của pt là S = { -1 ; 2 }
b, \(\frac{5}{3}\sqrt{15x}-\sqrt{15x}-2=\frac{1}{3}\sqrt{15x}\)ĐK : \(x\ge0\)
\(\Leftrightarrow\frac{2}{3}\sqrt{15x}-2=\frac{1}{3}\sqrt{15x}\Leftrightarrow\frac{1}{3}\sqrt{15x}=2\)
\(\Leftrightarrow\sqrt{15x}=6\)bình phương 2 vế : \(\Leftrightarrow15x=36\Leftrightarrow x=\frac{36}{15}=\frac{12}{5}\)( tm )
Vậy tập nghiệm của pt là S = { 12/5 }
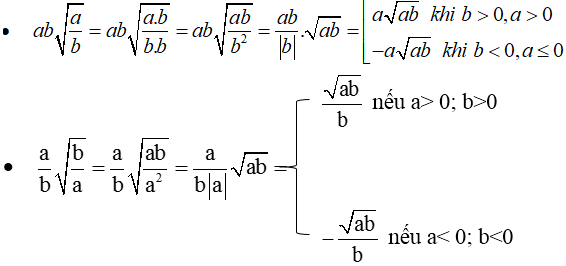

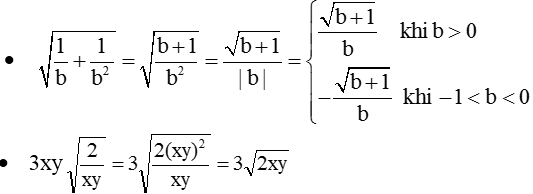
Ta có:
+) 3√5=√32.5=√9.5=√45.35=32.5=9.5=45.
+) −5√2=−√52.2=−√25.2=−√50.−52=−52.2=−25.2=−50.
+) Với xy>0xy>0 thì √xyxy có nghĩa nên ta có:
−23√xy=−√(23)2.xy=−√49xy.−23xy=−(23)2.xy=−49xy.
+) Với x>0x>0 thì √2x2x có nghĩa nên ta có:
x√2x=√x2.2x=√x2.2xx2x=x2.2x=x2.2x=√2x.xx=√2x.
a, \(3\sqrt{5}=\sqrt{9.5}=\sqrt{45}\)
b, \(-5\sqrt{2}=-\sqrt{25.2}=-\sqrt{50}\)
c, \(-\frac{2}{3}\sqrt{xy}=-\sqrt{\frac{4}{9}xy}\)
d, \(x\sqrt{\frac{2}{x}}=\sqrt{\frac{2x^2}{x}}=\sqrt{2x}\)