Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tâm O của đường tròn nội tiếp tam giác đều cũng là giao điểm ba đường trung tuyến, ba đường cao.
Do đó đường cao h=AE=3.OE=3cm.
Trong tam giác đều, h = a√3/2 (a là độ dài mỗi cạnh).
Suy ra 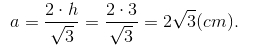 Do đó diện tích tam giác ABC là
Do đó diện tích tam giác ABC là
 Ta chọn (D).
Ta chọn (D).

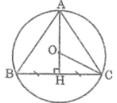
Vì O là tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của ba đường trung trực trong tam giác ABC.
Kẻ AH ⊥ BC. Ta có: O ∈ AH
Trong tam giác vuông ABH, ta có:
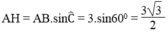
Vì tam giác ABC đều nên AH là đường cao cũng đồng thời là trung tuyến nên:
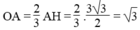
Vậy chọn đáp án C.

biết là bằng 9 rồi nhưng mà (Nhập kết quả dưới dạng số thập phân gọn nhất)
tính sao?????

NA/BA = NC/BC
Vì Tam giác ABC vuông tại A, biết AB=3cm,BC=5cm => AC= 4(cm)
=> NC-NA=4 (cm)
=> NC/BC = NA/BA = ( NC-NA)/(BC-AB) = 2
=> NA= BA*2 =6 (cm)

Ta có:
12+√3+12−√312+3+12−3
=2−√3(2+√3)(2−√3)+2+√3(2−√3)(2+√3)=2−3(2+3)(2−3)+2+3(2−3)(2+3)
=2−√322−(√3)2+2+√322−(√3)2=2−322−(3)2+2+322−(3)2
=2−√34−3+2+√34−3=2−34−3+2+34−3
=2−√31+2+√31=2−31+2+31
=2−√3+2+√3=4=2−3+2+3=4.
Chọn đáp án (D). 44
Ta có : \(\frac{1}{2+\sqrt{3}}+\frac{1}{2-\sqrt{3}}=\frac{2-\sqrt{3}+2+\sqrt{3}}{4-3}=4\)
Vậy chọn D

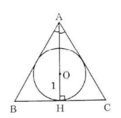
- Chọn D.
- Gọi O là tâm đường tròn nội tiếp Δ ABC, H là tiếp điểm thuộc BC.
Đường phân giác AO của góc A cũng là đường cao nên A, O, H thẳng hàng.
Ta có: HB = BC, ∠HAC = 30o, AH = 3.OH = 3 (cm)
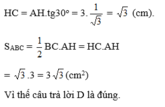

Cho tam giác đều ABC ngoại tiếp đường tròn bán kính 11cm. Diện tích của tam giác ABCABC bằng:
A. \(6cm^2\) ; B. \(\sqrt{3}cm^2\) ;
C.\(\frac{3\sqrt{3}}{4}cm^2\) ; D. \(3\sqrt{3cm^2}\)
Câu trả lời đúng là D.
Gọi OO là tâm đường tròn nội tiếp tam giác đều ABCABC, HH là tiếp điểm thuộc BCBC.
Đường phân giác AOAO của góc AA cũng là đường cao nên AA, OO, HH thẳng hàng.
\mathrm{HB}=\mathrm{HC}HB=HC, \widehat{HAC}=30^{\circ}HAC=30∘
AH=3\cdot OH=3AH=3⋅OH=3(cm)
HC=AH \cdot tan 30^{\circ}=3 \cdot \dfrac{1}{\sqrt{3}}=\sqrt{3}HC=AH⋅tan30∘=3⋅31=3(cm)
S_{ABC}=\dfrac{1}{2} BC.AH=HC.AH=3 \sqrt{3}SABC=21BC.AH=HC.AH=33(cm^{2}2)
Vì thế, câu trả lời (D) là đúng.