Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tâm O của đường tròn nội tiếp tam giác đều cũng là giao điểm ba đường trung tuyến, ba đường cao.
Do đó đường cao h=AE=3.OE=3cm.
Trong tam giác đều, h = a√3/2 (a là độ dài mỗi cạnh).
Suy ra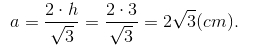 
Do đó diện tích tam giác ABC là
Ta chọn (D).
Gọi O là giao 3 đường trung trực của ∆ABC. Khi đó O là tâm đường tròn ngoại tiếp ∆ABC. Gọi H là giao điểm của AO và BC. Ta có : AH = 3 cm
OA = 2 3 AH = 2 3 3 cm
bán kính đường tròn ngoại tiếp tam giác đều bằng 2/3 đường cao tam giác đều
đường cao của tam giác trên = \(\sqrt{\left(\left(5\sqrt{3}\right)^2-\left(\frac{1}{2}.5\sqrt{3}\right)^2\right)}\) =7,5
suy ra R=2/3 . 7,5= 5
Làm thế làm zì cho khổ ...hả LDM
Tính S tam giác đều:\(\frac{x^2\sqrt{3}}{4}\), thay x =5 căn 3 vào , tính S
.. tính lun Bán kính: R = \(\frac{abc}{4S}\), a;b;c là các cạnh tam giác đều, thay S tính dc ,tacos R = 5cm
NA/BA = NC/BC
Vì Tam giác ABC vuông tại A, biết AB=3cm,BC=5cm => AC= 4(cm)
=> NC-NA=4 (cm)
=> NC/BC = NA/BA = ( NC-NA)/(BC-AB) = 2
=> NA= BA*2 =6 (cm)
biết là bằng 9 rồi nhưng mà (Nhập kết quả dưới dạng số thập phân gọn nhất)
tính sao?????
Vì O là tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của ba đường trung trực trong tam giác ABC.
Kẻ AH ⊥ BC. Ta có: O ∈ AH
Trong tam giác vuông ABH, ta có:
Vì tam giác ABC đều nên AH là đường cao cũng đồng thời là trung tuyến nên:
Vậy chọn đáp án C.