Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

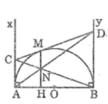
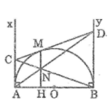
a) Ax, By là các tiếp tuyến của đường tròn (O)
=> Ax // By (cùng vuông góc với AB)
=> AMNB là hình thang
Hình thang AMNB có: OA = OB; IM = IN
=> OI là đường trung bình
=> OI // AM // BN
Lại có: AM, BN vuông góc với AB
=> IO vuông góc với AB
=> AB là tiếp tuyến của đường tròn (I;IO)

O A H B C M y D x N
\(Ax\perp AB\)
\(By\perp AB\)
Suy ra: Ax // By hay AC // BD
Trong tam giác BND, ta có AC // BD
Suy ra: \(\frac{ND}{NA}=\frac{BD}{AC}\) ( hệ quả định lí Ta-lét ) (1)
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = CM và BD = DM (2)
Từ (1) và (2) suy ra: \(\frac{ND}{NA}=\frac{MD}{MC}\)
Trong tam giác ACD, ta có: \(\frac{ND}{NA}=\frac{MD}{MC}\)
Suy ra: MN // AC (theo định lí đảo định lí Ta-lét)
Mà: \(AC\perp AB\) ( vì \(Ax\perp AB\) )
Suy ra: \(MN\perp AB\)
b. Trong tam giác ACD, ta có: MN // AC
Suy ra: \(\frac{MN}{AC}=\frac{DN}{DA}\)( hệ quả định lí Ta-lét ) (3)
Trong tam giác ABC, ta có: MH // AC ( vì M, N, H thẳng hàng )
Suy ra: \(\frac{HN}{AC}=\frac{BN}{BC}\)( hệ quả định lí Ta-lét ) (4)
Trong tam giác BDN, ta có: AC // BD
Suy ra: \(\frac{ND}{NA}=\frac{BN}{NC}\) ( hệ quả định lí Ta-lét )
\(\Rightarrow\frac{ND}{\left(DN+NA\right)}=\frac{BN}{BN+NC}\Leftrightarrow\frac{ND}{DA}=\frac{BN}{BC}\left(5\right)\)
Từ (3), (4) và (5) suy ra: \(\frac{MN}{AC}=\frac{HN}{AC}\Rightarrow MN=HN\)

Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Trong tam giác BND, ta có AC // BD
Suy ra: ND/NA = BD/AC (hệ quả định lí Ta-lét) (1)
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = CM và BD = DM (2)
Từ (1) và (2) suy ra: ND/NA = MD/MC
Trong tam giác ACD, ta có: ND/NA = MD/MC
Suy ra: MN // AC (theo định lí đảo định lí Ta-lét)
Mà: AC ⊥ AB (vì Ax ⊥ AB)
Suy ra: MN ⊥ AB

Trong tam giác ACD, ta có: MN // AC
Suy ra: MN/AC = DN/DA (hệ quả định lí Ta-lét) (3)
Trong tam giác ABC, ta có: MH // AC (vì M, N, H thẳng hàng)
Suy ra: HN/AC = BN/BC (hệ quả định lí Ta-lét) (4)
Trong tam giác BDN, ta có: AC // BD
Suy ra: ND/NA = BN/NC (hệ quả định lí Ta-lét)
⇒ ND/(DN + NA) = BN/(BN + NC) ⇔ ND/DA = BN/BC (5)
Từ (3), (4) và (5) suy ra: MN/AC = HN/AC ⇒ MN = HN

A H O B N C M D x y
Ax \(\perp\) AB
By \(\perp\) AB
Suy ra: Ax // By hay AC // BD
Trong tam giác BND, ta có AC // BD
Suy ra: \(\frac{ND}{NA}=\frac{BD}{AC}\)(hệ quả định lí Ta-lét) (1)
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = CM và BD = DM (2)
Từ (1) và (2) suy ra: \(\frac{ND}{NA}=\frac{MD}{MC}\)
Trong tam giác ACD, ta có: \(\frac{ND}{NA}=\frac{MD}{MC}\)
Suy ra: MN // AC (theo định lí đảo định lí Ta-lét)
Mà: AC \(\perp\) AB (vì Ax \(\perp\) AB)
Suy ra: MN \(\perp\) AB
b. Trong tam giác ACD, ta có: MN // AC
Suy ra: \(\frac{MN}{AC}=\frac{DN}{DA}\) (hệ quả định lí Ta-lét) (3)
Trong tam giác ABC, ta có: MH // AC (vì M, N, H thẳng hàng)
Suy ra: \(\frac{HN}{AC}=\frac{BN}{BC}\) (hệ quả định lí Ta-lét) (4)
Trong tam giác BDN, ta có: AC // BD
Suy ra: \(\frac{ND}{NA}=\frac{BN}{NC}\) (hệ quả định lí Ta-lét)
\(\Rightarrow\frac{ND}{\left(DN+NA\right)}=\frac{BN}{\left(BN+NC\right)}\Leftrightarrow\frac{ND}{DA}=\frac{BN}{BC}\left(5\right)\)
Từ (3), (4) và (5) suy ra: MN/AC = HN/AC => MN = HN
a: Xét hình thang AMNB có
O,I lần lượtlà trung điểm của AB,MN
nên OI là đường trung bình
=>OI//AM//NB
=>OI vuông góc với AB
=>AB là tiếp tuyến của (I;IO)
b: Gọi giao của NO và MA là E
Xét ΔOAE vuông tại A và ΔOBN vuông tại B có
OA=OB
góc AOE=góc BON
Do đo: ΔOAE=ΔOBN
=>OE=ON
Xét ΔMEN có
MO vừa là đường cao, vừa là trung tuyến
nên ΔMEN cân tại M
=>MO là phân giác của góc AMN