Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét hình thang AMNB có
O,I lần lượtlà trung điểm của AB,MN
nên OI là đường trung bình
=>OI//AM//NB
=>OI vuông góc với AB
=>AB là tiếp tuyến của (I;IO)
b: Gọi giao của NO và MA là E
Xét ΔOAE vuông tại A và ΔOBN vuông tại B có
OA=OB
góc AOE=góc BON
Do đo: ΔOAE=ΔOBN
=>OE=ON
Xét ΔMEN có
MO vừa là đường cao, vừa là trung tuyến
nên ΔMEN cân tại M
=>MO là phân giác của góc AMN

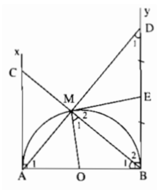
Tam giác EBM cân nên ∠ M 2 = ∠ B 2 . Suy ra ∠ M 1 + ∠ M 2 = ∠ B 1 + ∠ B 2 = 90 ° , tức là ME ⊥ OM tại M. Vậy ME là tiếp tuyến của nửa đường tròn.

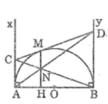
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Trong tam giác BND, ta có AC // BD
Suy ra: ND/NA = BD/AC (hệ quả định lí Ta-lét) (1)
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = CM và BD = DM (2)
Từ (1) và (2) suy ra: ND/NA = MD/MC
Trong tam giác ACD, ta có: ND/NA = MD/MC
Suy ra: MN // AC (theo định lí đảo định lí Ta-lét)
Mà: AC ⊥ AB (vì Ax ⊥ AB)
Suy ra: MN ⊥ AB

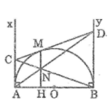
Trong tam giác ACD, ta có: MN // AC
Suy ra: MN/AC = DN/DA (hệ quả định lí Ta-lét) (3)
Trong tam giác ABC, ta có: MH // AC (vì M, N, H thẳng hàng)
Suy ra: HN/AC = BN/BC (hệ quả định lí Ta-lét) (4)
Trong tam giác BDN, ta có: AC // BD
Suy ra: ND/NA = BN/NC (hệ quả định lí Ta-lét)
⇒ ND/(DN + NA) = BN/(BN + NC) ⇔ ND/DA = BN/BC (5)
Từ (3), (4) và (5) suy ra: MN/AC = HN/AC ⇒ MN = HN
a) Ax, By là các tiếp tuyến của đường tròn (O)
=> Ax // By (cùng vuông góc với AB)
=> AMNB là hình thang
Hình thang AMNB có: OA = OB; IM = IN
=> OI là đường trung bình
=> OI // AM // BN
Lại có: AM, BN vuông góc với AB
=> IO vuông góc với AB
=> AB là tiếp tuyến của đường tròn (I;IO)
b) Góc AMO = góc MOI (cùng phụ góc MOA) (1)
Tam giác MON vuông tại M có OI là đường trung tuyến
=> OI = MI = IN
=> tgiac MIO cân tại I
=> góc IMO = góc MOI (2)
Từ (1) và (2) => góc AMO = góc IMO
=> MO là phân gics góc AMN