Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
Gọi x, y lần lượt là số giờ đạp xe và tập tạ trong một tuần.
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Số giờ tập thể dục tối đa là 12 giờ nên \(x + y \le 12\)
- Tổng số calo tiêu hao một tuần không quá 7000 calo nên \(350x + 700y \le 7000\)
Từ đó ta có hệ bất phương trình: \(\left\{ \begin{array}{l}x + y \le 12\\350x + 700y \le 7000\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.

Miền không gạch chéo (miền tứ giác OABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.
Với các đỉnh \(O(0;0),\)\(A(0;10),\)\(B(4;8),\)\(C(12;0).\)
a) Gọi F là chi phí luyện tập (đơn vị: nghìn đồng), ta có: \(F = 50y\)
Tính giá trị của F tại các đỉnh của tứ giác:
Tại \(O(0;0),\)\(F = 50.0 = 0\)
Tại \(A(0;10),\)\(F = 50.10 = 500\)
Tại \(B(4;8),\)\(F = 50.8 = 400\)
Tại \(C(12;0).\)\(F = 50.0 = 0\)
F đạt giá trị nhỏ nhất bằng 0 tại \(O(0;0),\)\(C(12;0).\)
Vậy bạn Mạnh cần đạp xe 12 giờ hoặc không tập thể dục..
b) Gọi T là lượng calo tiêu hao (đơn vị: calo), ta có: \(T = 350x + 700y\)
Tính giá trị của F tại các đỉnh của tứ giác:
Tại \(O(0;0),\)\(T = 350.0 + 700.0 = 0\)
Tại \(A(0;10),\)\(T = 350.0 + 700.10 = 7000\)
Tại \(B(4;8),\)\(T = 350.4 + 700.8 = 7000\)
Tại \(C(12;0),\)\(T = 350.12 + 700.0 = 4200\)
T đạt giá trị lớn nhất bằng 7000 tại \(A(0;10),\)\(B(4;8).\)
Vậy bạn Mạnh có thể chọn một trong hai phương án: Tập tạ 10 giờ hoặc đạp xe 4 tiếng và tập tạ 8 tiếng.

Để xác định điểm M ta cần giải hệ phương trình gồm hai phương trình đường thẳng của hai đường thẳng a và b

Để xác định tọa độ của máy bay ta phải lập phương trình quỹ đạo bay của máy bay hay chính là lập phương trình đường thẳng.

a) Phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\)
b) Thay \(t = 2\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.2 = 81\\y = 1 + 30.2 = 61\end{array} \right.\)
Vậy khi \(t = 2\) thì tọa độ của ô tô là \(\left( {81;61} \right)\)
Thay \(t = 4\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.4 = 161\\y = 1 + 30.4 = 121\end{array} \right.\)
Vậy khi \(t = 4\) thì tọa độ của ô tô là \(\left( {161;121} \right)\)

Để xác định tọa độ của máy bay trực thăng ta sử dụng biểu thức tọa độ của 2 vectơ

a) Nam có là một phần tử của tập hợp A
Ngân không là một phần tử của tập hợp B
b) \(A = \){Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
\(B = \){Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}

X = {Khánh; Bình; Hương; Chi; Tú}
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Dễ thấy: Các phần tử của X đều là phần tử của tập hợp A và tập hợp B.
Do đó \(X \subset A\) và \(X \subset B\).
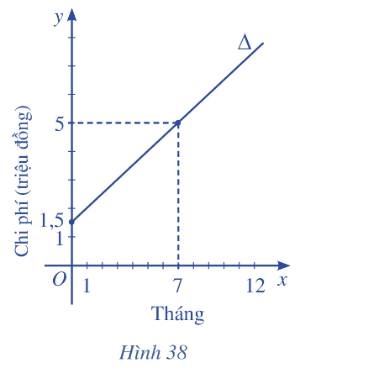



a) Đường thẳng \(\Delta \) đi qua hai điểm lần lượt có tọa độ \(\left( {0;1,5} \right),\left( {7;5} \right)\) nên \(\Delta \) có phương trình là:
\(\frac{{x - 0}}{{7 - 0}} = \frac{{y - 1,5}}{{5 - 1,5}} \Leftrightarrow \frac{x}{7} = \frac{{y - 1,5}}{{3,5}} \Leftrightarrow x - 2y + 3 = 0\)
b) Giao điểm của đường thẳng \(\Delta \) với trục \(Oy\) ứng với \(x = 0\). Thời điểm \(x = 0\)cho biết khoản phí tham gia ban đầu mà người tập phải trả. Khi \(x = 0\) thì \(y = 1,5\) , vì vậy khoản phí tham gia ban đầu mà người tập phải trả là 1 500 000 đồng.
c) 12 tháng đầu tiên ứng với \(x = 12\)
Từ phương trình đường thẳng \(\Delta \) ta có: \(x - 2y + 3 = 0 \Leftrightarrow y = \frac{1}{2}x + \frac{3}{2}\)
Thay \(x = 12\) vào phương trình đường thẳng ta có: \(y = \frac{1}{2}.12 + \frac{3}{2} = 7.5\)
Vậy tổng chi phí mà người đó phải trả khi tham gia phòng tập thể dục trong 12 tháng là 7tr5 nghìn đồng.