Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đỉnh parabol : \(I\left(1;-m^2-m-2\right)\) nằm trên đt y = x - 3 \(\Leftrightarrow x=1;y=-m^2-m-2\) t/m ct h/s :
\(-m^2-m-2=1-3\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-1\end{matrix}\right.\)(loại m = 0)

\(y=mx^2-2mx-m^2-1\)
\(=m\left(x^2-2x\right)-m^2-1\)
Điểm cố định của (d) có tọa độ là:
\(\left\{{}\begin{matrix}x^2-2x=0\\y=-m^2-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\left(x-2\right)=0\\y=-m^2-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{0;2\right\}\\y=-m^2-1\end{matrix}\right.\)
TH1: x=0
Thay x=0 và \(y=-m^2-1\) vào y=x-2, ta được:
\(-m^2-1=0-2=-2\)
=>\(m^2+1=2\)
=>\(m^2=1\)
=>\(\left[{}\begin{matrix}m=1\\m=-1\end{matrix}\right.\)
TH2: x=2
Thay x=2 và \(y=-m^2-1\) vào y=x-2, ta được:
\(-m^2-1=2-2=0\)
=>\(m^2+1=0\)
=>\(m^2=-1\)(vô lý)

Để hai đường thẳng d1; d2 cắt nhau tại một điểm nằm trên d3 khi và chỉ khi 3 đường thẳng d1; d2; d3 đồng quy.
Giao điểm của d1 và d3 là nghiệm hệ phương trình:
x − 2 y + 1 = 0 x + y − 5 = 0 ⇔ x = 3 y = 2 ⇒ A ( 3 ; 2 )
Do 3 đường thẳng này đồng quy nên điểm A thuộc d2. Suy ra:
3m - (3m-2).2 + 2m – 2= 0
⇔ 3m – 6m + 4 + 2m – 2 = 0 ⇔ - m + 2 = 0 ⇔ m= 2
Với m= 2 thì đường thẳng d2 : 2x - 4y + 2= 0 hay x- 2y + 1 =0 . Khi đó, đường thẳng d1 và d2 trùng nhau.
Vậy không có giá trị nào của m thỏa mãn.
ĐÁP ÁN D

Gọi (P):y=x2-2mx+m+3 (D):y=x+2
Cho S là điểm thấp nhất của đồ thị hàm số (P)
xs=\(-\dfrac{b}{2a}=-\dfrac{-2m}{2.1}\)=m
yS=-delta/4=\(-\dfrac{b^2-4ac}{4a}=-\dfrac{\left(-2m\right)^2-4\left(m+3\right)}{4}=-\dfrac{4m^2-4m-12}{4}\)=-m2+m+3
Vậy tọa độ đỉnh là S(m;-m2+m+3)
Theo đề bài thì S thuộc (D) khi yS=xS+2
thế vào ta có -m2+m+3=m+2
tương đương: m2=1 suy ra m=1 (nhận) hoặc m=-1 (loại) vì m>0
Vậy hàm số (P):y=m2-2x+4
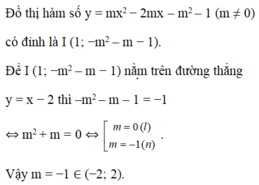



\(\Delta'=m^2+m\left(m^2+1\right)=m^3+m^2+m\)
Tọa độ đỉnh \(I\left(-\frac{b}{2a};-\frac{\Delta'}{a}\right)\Rightarrow I\left(1;-m^2-m-1\right)\)
Để I thuộc d \(\Rightarrow-m^2-m-1=1-2\)
\(\Leftrightarrow m^2+m=0\Rightarrow\left[{}\begin{matrix}m=0\left(l\right)\\m=-1\end{matrix}\right.\)