Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì trong 5 người được chọn phải có ít nhất 1 nữ và ít nhất phải có 2 nam nên số học sinh nữ gồm 1 hoặc 2 hoặc 3 nên ta có các trường hợp sau:
- Chọn 1 nữ và 4 nam.
+) Số cách chọn 1 nữa: 5 cách
+) Số cách chọn 2 nam làm đội trưởng và đội phó: A 15 2
+) Số cách chọn 2 nam còn lại: C 13 2
Suy ra có 5 A 15 2 C 13 2 cách chọn cho trường hợp này.
- Chọn 2 nữ và 3 nam.
+) Số cách chọn 2 nữ: C 5 2 cách.
+) Số cách chọn 2 nam làm đội trưởng và đội phó: A 15 2 cách.
+) Số cách chọn 1 còn lại: 13 cách.
Suy ra có 13 A 15 2 C 5 2 cách chọn cho trường hợp này.
- Chọn 3 nữ và 2 nam.
+) Số cách chọn 3 nữ : C 5 3 cách.
+) Số cách chọn 2 làm đội trưởng và đội phó: A 15 2 cách.
Suy ra có A 15 2 C 5 2 cách chọn cho trường hợp 3.
Vậy có 5 A 15 2 C 13 2 + 13 A 15 2 . C 5 2 + A 15 2 . C 5 3 = 111300 cách.
Chọn đáp án D.

Vì trong 5 người được chọn phải có ít nhất 1 nữ và ít nhất phải có 2 nam nên số học sinh nữ gồm 1 hoặc 2 hoặc 3 nên ta có các trường hợp sau:
chọn 1 nữ và 4 nam.
+) Số cách chọn 1 nữa: 5 cách
+) Số cách chọn 2 nam làm đội trưởng và đội phó: ![]()
+) Số cách chọn 2 nam còn lại: ![]()
Suy ra có ![]() cách chọn cho trường hợp này.
cách chọn cho trường hợp này.
chọn 2 nữ và 3 nam.
+) Số cách chọn 2 nữ: ![]() cách.
cách.
+) Số cách chọn 2 nam làm đội trưởng và đội phó: ![]() cách.
cách.
+) Số cách chọn 1 còn lại: 13 cách.
Suy ra có ![]() cách chọn cho trường hợp này.
cách chọn cho trường hợp này.
Chọn 3 nữ và 2 nam.
+) Số cách chọn 3 nữ : ![]() cách.
cách.
+) Số cách chọn 2 làm đội trưởng và đội phó: ![]() cách.
cách.
Suy ra có ![]() cách chọn cho trường hợp 3.
cách chọn cho trường hợp 3.
Vậy có ![]() cách.
cách.
Chọn D.

Vì trong 5 người được chọn phải có ít nhất 1 nữ và ít nhất phải có 2 nam nên số học sinh nữ gồm 1 hoặc 2 hoặc 3 nên ta có các trường hợp sau:
Chọn 1 nữ và 4 nam.
+) Số cách chọn 1 nữa: 5 cách
+) Số cách chọn 2 nam làm đội trưởng và đội phó: A 15 2
+) Số cách chọn 2 nam còn lại: C 13 2
Suy ra có 5 A 15 2 . C 13 2 cách chọn cho trường hợp này.
Chọn 2 nữ và 3 nam.
+) Số cách chọn 2 nữ: C 5 2 cách.
+) Số cách chọn 2 nam làm đội trưởng và đội phó: A 15 2 cách.
+) Số cách chọn 1 còn lại: 13 cách.
Suy ra có 13 A 15 2 . C 5 2 cách chọn cho trường hợp này.
Chọn 3 nữ và 2 nam.
+) Số cách chọn 3 nữ : C 5 3 cách.
+) Số cách chọn 2 làm đội trưởng và đội phó: A 15 2 cách.
Suy ra có A 15 2 . C 5 3 cách chọn cho trường hợp 3.
Vậy có 5 A 15 2 . C 13 2 + 13 A 15 2 . C 5 2 + A 15 2 . C 5 3 = 111300 cách.
Chọn đáp án D

Đáp án D
Tổng số cách chọn 8 em từ đội 18 người là ![]()
Số cách chọn 8 em từ khối 12 và khối 11 là ![]()
Số cách chọn 8 em từ khối 11 và khối 10 là ![]()
Số cách chọn 8 em từ khối 10 và khối 12 là ![]()
Vậy số cách chọn để có các em ở cả 3 khối là
![]()

Chọn C
+ Chia đều 16 đội vào 4 bảng có ![]()
+ Sắp xếp 3 đội của 3 lớp Toán vào 3 bảng khác nhau trong 4 bảng có A 4 3 cách.
Chọn 3 đội trong 13 đội còn lại để xếp vào bảng có đội lớp 10 Toán có C 13 3 cách.
Chọn 3 đội trong 10 đội còn lại để xếp vào bảng có đội lớp 11 Toán có C 10 3 cách.
Chọn 3 đội trong 7 đội còn lại để xếp vào bảng có đội lớp 12 Toán có C 7 3 cách.
Bốn đội còn lại xếp vào bảng còn lại.
Suy ra số cách chia đều 16 đội vào 4 bảng sao cho 3 đội của 3 lớp Toán nằm ở 3 bảng khác nhau là ![]()
+ Xác suất cần tìm là: 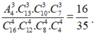

+ Số cách chọn 6 học sinh bất kỳ từ 18 học sinh là. C 18 6 = 18564
+ Tiếp theo ta đếm số cách chọn ra 6 học sinh từ các học sinh trên mà không có đủ cả ba khối. Khi đó có ba phương án như dưới đây.
Phương án 1: 6 học sinh được chọn thuộc vào khối 10 hoặc 11, số cách chọn là C 13 6 = 1716
Phương án 2: 6 học sinh được chọn thuộc vào cả hai khối 10 và 12, số cách chọn là C 12 6 - C 7 6 = 917
Phương án 3: 6 học sinh được chọn thuộc vào cả hai khối 11 và 12, số cách chọn là C 11 6 - C 6 6 = 461
Vậy số cách chọn 6 học sinh sao cho mỗi khối có ít nhất một học sinh là:
18564 – (1716 + 917 + 461) = 15470.
chọn D.

Không gian mẫu: \(C_9^3.C_6^3\)
Chia 3 bạn nữ vào 3 tổ: \(3!\) cách
Xếp 6 bạn nam vào 3 tổ: \(C_6^2.C_4^2\) cách
Xác suất: \(P=\dfrac{3!.C_6^2.C_4^2}{C_9^3.C_6^3}\)

Chọn A.
Chọn ngẫu nhiên 5 học sinh trong số 48 học sinh có:![]()
- Gọi A là biến cố "chọn 5 học sinh trong đó có ít nhất một học sinh nữ" thì ![]() là biến cố "chọn 5 học sinh mà trong đó không có học sinh nữ".
là biến cố "chọn 5 học sinh mà trong đó không có học sinh nữ".
- Ta có số kết quả thuận lợi cho ![]() là:
là:
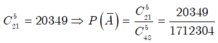
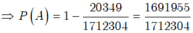

Đáp án A
Chọn 3 tiết mục bất kỳ có: Ω = C 9 3 = 84 cách.
Gọi A là biến cố: “ba tiết mục được chọn có đủ cả ba khối và đủ cả ba nội dung”.
Khối 10 chọn 1 tiết mục có 3 cách
khối 11 chọn 1 tiết mục khác khối 10 có 2 cách
tương tự khối 12 có 1 cách
Ta có: Ω A = 3 . 2 . 1 = 6 cách
Vậy P = 6 84 = 1 14
chọn 5 đội trong 12 đội có \(C^5_{12}=792\) cách
=> \(n\left(\Omega\right)=792\)
Gọi A:" 5 đội được chọn có ít nhất 1 đội cờ đỏ khối 10 và ít nhất 1 đội cờ đỏ khối 11 "
+) 1 đội K10 +4 đội K11 => có \(C^1_5.C^4_7=175\) cách
+) 2 đội K10 +3 đội K11 => có \(C^2_5.C^3_7=350\)cách
+) 3 đội k10 + 2 đội k11 => có \(C^3_5.C^2_7=210\) cách
+) 4 độ k10 + 1 đội k11 => có \(C^4_5.C^1_7=35\)cách
=> n(A) = 175+350+210+35 = 770
=> P(A) = 770/792=35/36