Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^2-2\cdot x\cdot\left(m-1\right)+2m-3=0\)
Ta có \(\Delta=4\cdot\left(m-1\right)^2-4\cdot\left(2m-3\right)\)
\(\Leftrightarrow\Delta=4m^2-16m+16=4\cdot\left(m-2\right)^2\ge0\forall m\)
+) Khi \(\Delta=0\Leftrightarrow m=2\Leftrightarrow x_1=x_2=\frac{2\cdot\left(m-1\right)}{2}=m-1=1\)
Khi đó \(x_1^2-2x_2=-1\) ( loại )
+) Khi \(\Delta>0\Leftrightarrow\left[{}\begin{matrix}x_1=\frac{2\cdot\left(m-1\right)+\sqrt{4\left(m-2\right)^2}}{2}=m-1+\left|m-2\right|\\x_2=\frac{2\cdot\left(m-1\right)-\sqrt{4\left(m-2\right)^2}}{2}=m-1-\left|m-2\right|\end{matrix}\right.\)
* Xét \(m\ge2\Leftrightarrow\left[{}\begin{matrix}x_1=2m-3\\x_2=1\end{matrix}\right.\)
\(\Rightarrow\left(2m-3\right)^2-2=7\Leftrightarrow\left(2m-3\right)^2=9\Leftrightarrow\left[{}\begin{matrix}m=3\left(chon\right)\\m=0\left(loai\right)\end{matrix}\right.\)
* Xét \(m< 2\Leftrightarrow\left[{}\begin{matrix}x_1=1\\x_2=2m-3\end{matrix}\right.\)
\(\Rightarrow1-2\cdot\left(2m-3\right)=7\Leftrightarrow m=0\left(chon\right)\)
Vậy \(m\in\left\{0;3\right\}\) thì phương trình có 2 nghiệm thỏa mãn.
\(x^2-2\left(m-1\right)x+2m-3=0\)
( Δ'=b'^2-ac = \(\left(m-2\right)^2\)\(\ge0\) ∀ m ϵ R)
\(\Leftrightarrow x^2-2mx+2x+2m-3=0\)
\(\Leftrightarrow x^2-2mx+3x-x+2m-3=0\)
\(\Leftrightarrow x^2-x-2mx+2m+3x-3=0\)
\(\Leftrightarrow x\left(x-1\right)-2m\left(x-1\right)+3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2m+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-1=0\\x-2m+3=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x_{ }=1\\x_{ }=2m-3\end{matrix}\right.\)(*)
Thay (*) vào điều kiện \(x_1^2-2x_2=7\)
Ta được 2 trường hợp :
Với \(\left[{}\begin{matrix}x_1=1\\x_2=2m-3\end{matrix}\right.\)
Thay vào (*) được m=0 (1)
TH2: \(\left[{}\begin{matrix}x_1=2m-3\\x_2=1\end{matrix}\right.\)
Ta thay vào (*) và tính được :
\(\left[{}\begin{matrix}m=0\\m=3\end{matrix}\right.\)(2)
Từ (1) và (2) suy ra \(\left[{}\begin{matrix}m=0\\m=3\end{matrix}\right.\)thỏa mãn điều kiện.

Vì phương trình có 2 nghiệm x1;x2
=> Theo vi-ét ta có
x1 + x2 = 2(m+1) và x1x2 = 2m+3
theo bài ra ta có
(x1 - x2)2 = 4
<=> x12 - 2x1x2 + x22 = 4
<=> x12 + 2x1x2 + x22 - 4x1x2 = 4
<=> (x1 + x2)2 - 4x1x2 = 4
<=> 4(m+1)2 - 4(2m+3) = 4
<=> (m+1)2 - (2m+3) = 1
<=> m2 + 2m +1 -2m -3 -1 = 0
<=> m2 - 3 = 0
<=> m2 = 3
<=> m\(=\pm\sqrt{3}\)
Vậy với m\(=\pm\sqrt{3}\) thì phương trình có hai nghiệm x1;x2 thỏa mãn (x1 - x2)2 = 4

\(\left(m+1\right)x^2-2\left(m-1\right)x+m-3=0\) (1)
a) Phương trình (1) có 2 nghiệm phân biệt khi và chỉ khi:
\(\Delta'=\left(m-1\right)^2-\left(m+1\right)\left(m-3\right)>0\)
\(\Leftrightarrow\left(m^2-2m+1\right)-\left(m^2-2m-3\right)>0\)
\(\Leftrightarrow4>0\)(luôn đúng)
Vậy phương trình có 2 nghiệm phân biệt với mọi m.
b) Để t nghĩ tí

\(a)\) Ta có : \(\Delta=\left(-m\right)^2-4\left(m-3\right)=m^2-4m+12=\left(m^2-4m+4\right)+8=\left(m-2\right)^2+8>0\)
Vậy pt (1) có hai nghiệm phân biệt với mọi m
\(b)\) Có \(x_1^2+x_2^2=5\)\(\Leftrightarrow\)\(\left(x_1+x_2\right)^2-2x_1x_2=5\) (*)
Theo định lý Vi-et ta có : \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=m-3\end{cases}}\)
(*) \(\Leftrightarrow\)\(m^2-2\left(m-3\right)=5\)
\(\Leftrightarrow\)\(m^2-2m+1=0\)
\(\Leftrightarrow\)\(m=1\)
Vậy để \(x_1^2+x_2^2=5\) thì \(m=1\)
\(c)\)......... -_-
Theo hệ thức Vi et( ý b) \(\hept{\begin{cases}X_1+X_2=m\\X_1.X_2=m-3\end{cases}\Rightarrow}X_1.X_2=X_1+X_2-3\)(thế \(X_1+X_2=m\)vô phương trình dưới)
Vậy hệ thức liên hệ giữa X1 X2 không chứa m là \(X_1X_2=X_1 +X_2-3\)

\(a,\Delta=m^2-4m+4=\left(m-2\right)^2\ge0\forall m\)
Nên pt đã cho luôn có 2 nghiệm phân biệt với mọi m
b, Theo Vi-ét \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=m-1\end{cases}}\)
Ta có \(B=\frac{2x_1x_2+3}{x_1^2+x_2^2+2\left(1+x_1x_2\right)}=1\)
\(\Leftrightarrow\frac{2x_1x_2+3}{\left(x_1+x_2\right)^2+2}=1\)
\(\Leftrightarrow\frac{2\left(m-1\right)+3}{m^2+2}=1\)
\(\Leftrightarrow\frac{2m+1}{m^2+2}=1\)
\(\Leftrightarrow2m+1=m^2+2\)
\(\Leftrightarrow m^2-2m+1=0\)
\(\Leftrightarrow\left(m-1\right)^2=0\)
\(\Leftrightarrow m=1\)
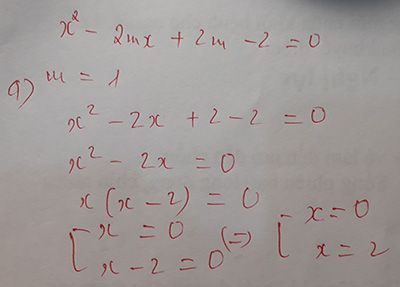
\(x^2-2x=1-m\)
\(\Rightarrow x_1^2-2x_1=1-m\)
Ta có:
\(x_1^2-2x_2+x_1.x_2=4\)
\(\Leftrightarrow x_1^2-2x_1+2\left(x_1-x_2\right)+x_1.x_2=4\)
\(\Leftrightarrow\left(1-m\right)+2\sqrt{\left(x_1+x_2\right)^2-4x_1.x_2}+m-1=4\)\(\left(x_1>x_2\right)\)
\(\Leftrightarrow\sqrt{4-4\left(m-1\right)}=2\)
\(\Rightarrow m=1\)
Vậy...............