K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 5 2019
1/ ĐKXĐ: \(cos2x\ne0\Rightarrow2x\ne k\frac{\pi}{2}\Rightarrow x\ne\frac{k\pi}{4}\)
2/ ĐKXĐ:
\(\sqrt{2-2cosx}\ne2\Rightarrow2-2cosx\ne4\)
\(\Rightarrow cosx\ne-1\Rightarrow x\ne\pi+k2\pi\)
3/ ĐKXĐ: \(sin3x\ne0\Rightarrow3x\ne k\pi\Rightarrow x\ne\frac{k\pi}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 5 2019
Khác nhau bạn
Ở câu 3, \(cot3x\) xác định nên \(sin3x\ne0\)
\(1-\sqrt{1+sin3x}\ne0\Rightarrow1+sin3x\ne1\Rightarrow sin3x\ne0\)
Cả 2 điều kiện xác định là cot3x xác đinh và mẫu xác định đều giống nhau là \(sin3x\ne0\)
HP
25 tháng 6 2021
1. \(sin\left(\dfrac{\pi}{3}-x\right)\ne0\Leftrightarrow\dfrac{\pi}{3}-x\ne k\pi\Leftrightarrow x\ne\dfrac{\pi}{3}-k\pi\)
2. \(cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
3. \(\sqrt{1+sinx}-\sqrt{2}\ge0\Leftrightarrow1+sinx\ge2\Leftrightarrow sinx\ge1\Leftrightarrow sinx=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
4. \(\sqrt{2-2cosx}-2\ne0\Leftrightarrow2-2cosx\ne4\Leftrightarrow cosx\ne-1\Leftrightarrow x\ne\pi+k2\pi\)
5. \(1-\sqrt{1+sin3x}\ne0\Leftrightarrow sin3x\ne0\Leftrightarrow3x\ne k\pi\Leftrightarrow x\ne\dfrac{k\pi}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 8 2020
Ít nhất thì bạn cũng phải nêu yêu cầu của đề bài là làm gì chứ bạn :)
NH
0
CM
11 tháng 12 2019
Điều kiện: 3x - 1 ≠ kπ ∀ k ∈ Z
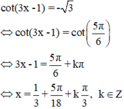
Mọi giá trị thuộc họ nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình có họ nghiệm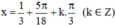 
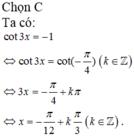
cot3x = tan2x
đkxđ: \(\left\{{}\begin{matrix}sin3x\ne0\\cos2x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{k\pi}{3}\\x\ne\frac{\pi}{4}+\frac{k\pi}{2}\end{matrix}\right.\)(k\(\in\)Z)
\(\Leftrightarrow\frac{cos3x}{sin3x}=\frac{sin2x}{cos2x}\)
\(\Leftrightarrow cos3x.cos2x=sin3x.sin2x\)
\(\Leftrightarrow cos3x.cos2x-sin3x.sin2x=0\)
\(\Leftrightarrow cos\left(3x+2x\right)=0\)
<=> \(5x=\frac{\pi}{2}+k\pi\)
<=> \(x=\frac{\pi}{10}+\frac{k\pi}{5}\)