
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(\left\{{}\begin{matrix}sin4x\ne0\\cos3x\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin4x\ne0\\4cos^3x-3cosx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin4x\ne0\\4cos^2x-3\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}sin4x\ne0\\2cos2x-1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin4x\ne0\\cos2x\ne\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ne\frac{k\pi}{4}\\x\ne\pm\frac{\pi}{6}+k\pi\end{matrix}\right.\)


\(1.\hept{\begin{cases}2-2\cos x\ge0\\\sqrt{2-2\cos x}-2\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}\cos x\le1\left(đ\right)\\\cos x\ne-1\end{cases}}\Leftrightarrow x\ne\pi+k2\pi\left(k\in Z\right)\)
\(2.\hept{\begin{cases}\sin3x\ne0\\1+\sin3x\ge0\\1-\sqrt{1+\sin3x}\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}3x\ne k\pi\\\sin3x\ge-1\left(đ\right)\\\sin3x\ne0\end{cases}}\Leftrightarrow x\ne\frac{k\pi}{3}\left(k\in Z\right)\)
\(3.\hept{\begin{cases}\sin2x\ne0\\\sin x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}2x\ne k\pi\\x\ne k\pi\end{cases}}\Leftrightarrow x\ne\frac{k\pi}{2}\left(k\in Z\right)\)

ĐKXĐ: ...
\(\Leftrightarrow\frac{sin4x}{cos4x}+\frac{sinx}{cosx}=\frac{2sin3x}{cos3x}\Leftrightarrow\frac{sin4x.cosx+cos4x.sinx}{cosx.cos4x}=\frac{2sin3x}{cos3x}\)
\(\Leftrightarrow sin5x.cos3x=2cosx.sin3x.cos4x\)
\(\Leftrightarrow\frac{1}{2}sin8x+\frac{1}{2}sin2x=\left(sin4x+sin2x\right)cos4x\)
\(\Leftrightarrow\frac{1}{2}sin8x+\frac{1}{2}sin2x=sin4x.cos4x+sin2x.cos4x\)
\(\Leftrightarrow\frac{1}{2}sin8x+\frac{1}{2}sin2x=\frac{1}{2}sin8x+sin2x.cos4x\)
\(\Leftrightarrow sin2x=2sin2x.cos4x\)
\(\Leftrightarrow sin2x\left(2cos4x-1\right)=0\)
Chưa học chứng minh 3 điểm thẳng hàng nên thắc mắc :D

a/ \(y'=tan4x+\left(x+1\right)\left(tan4x\right)'=tan4x+\frac{4\left(x+1\right)}{cos^24x}\)
b/ \(y'=2cos\left(sin\sqrt{x}\right)\left[cos\left(sin\sqrt{x}\right)\right]'=2cos\left(sin\sqrt{x}\right).\left(-sin\left(sin\sqrt{x}\right)\right)\left(sin\sqrt{x}\right)'\)
\(=-\frac{sin\left(2sin\sqrt{x}\right).cos\sqrt{x}}{2\sqrt{x}}\)
c/ \(y'=\frac{\left(sin2x\right)'}{cos^2\left(sin2x\right)}=\frac{2cos2x}{cos^2\left(sin2x\right)}\)

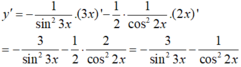
Ít nhất thì bạn cũng phải nêu yêu cầu của đề bài là làm gì chứ bạn :)