Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trần Trương Quỳnh Hoa và câu hỏi tương tự có đấy, tick cho mình nha!

\(ad=bc\Rightarrow ad:dc=bc:dc\Rightarrow\frac{ad}{dc}=\frac{bc}{dc}\Rightarrow\frac{a}{c}=\frac{b}{d}\)

Do ad = bc
=> \(\frac{ad}{cd}=\frac{bc}{cd}\)
=> \(\frac{a}{c}=\frac{b}{d}\left(đpcm\right)\)
Do ad = bc
\(\Rightarrow\frac{a}{d}=\frac{b}{c}\)
\(\Rightarrow ac=bd\)
\(\Rightarrow\frac{a}{c}=\frac{b}{d}\left(\text{đ}pcm\right)\)

\(ad=bc=>ad:dc=bc:dc=>\frac{ad}{dc}=\frac{bc}{dc}=>\frac{a}{c}=\frac{b}{d}\)

Ta có: ad = bc; c ≠ 0; d ≠ 0 suy ra cd ≠ 0
Chia cả 2 vế cho cd. Suy ra:
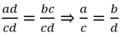

Ta có :
\(ad=bc\left(1\right)\)
Chia cả 2 vế của \(\left(1\right)\) cho \(bd\) ta được :
\(VT=\dfrac{ad}{bd}=\dfrac{a}{b}\left(2\right)\)
\(VP=\dfrac{bc}{bd}=\dfrac{c}{d}\left(3\right)\)
Từ \(\left(2\right)+\left(3\right)\Leftrightarrowđpcm\)
Từ có đẳng thức: \(ad=bc\)
\(\Rightarrow\dfrac{ad}{cd}=\dfrac{bc}{cd}\) \(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\) (đpcm)

Ta có: ad=bc (1)
Chia 2 vế của (1) cho bd ta có:
\(VT=\frac{ad}{bd}=\frac{a}{b}\left(2\right)\)
\(VP=\frac{bc}{bd}=\frac{c}{d}\left(2\right)\)
Từ (1) và (2) ta có: \(\frac{a}{b}=\frac{c}{d}\)
\(ad=bc=>ad:dc=bc:dc=>\frac{ad}{dc}=\frac{bc}{dc}=>\frac{a}{c}=\frac{b}{d}\)
\(ad=bc\Rightarrow\frac{ad}{cd}=\frac{bc}{cd}\Rightarrow\frac{a}{c}=\frac{b}{d}\)