
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


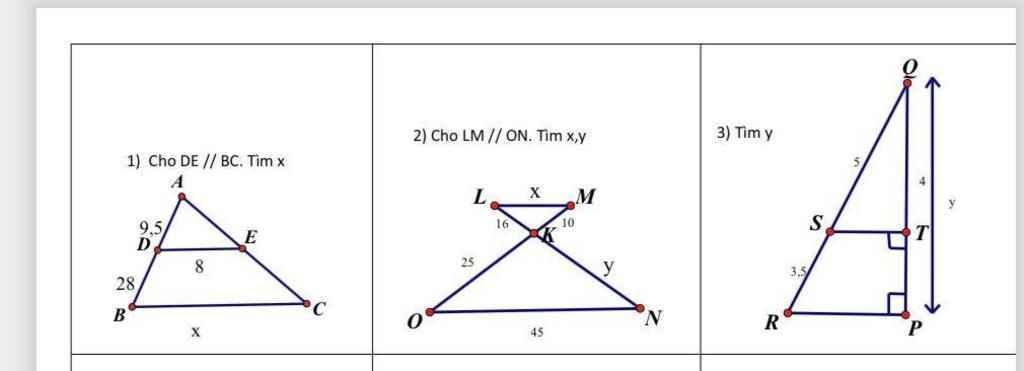
`1).`
Ta có: `AB=AD+DB=9,5+28=37,5`
`\triangle ABC` có: `DE////BC`, theo hệ quả của định lí Ta-lét:
`(AD)/(AB)=(DE)/(BC)`
`=>(9,5)/(37,5)=8/x`
`=>x=(37,5.8)/(9,5)`
`=>x=600/19`
`2).`
`\triangle OKN` có: `LM////ON` theo hệ quả của định lí Ta-lét:
`(KO)/(KM)=(KN)/(KL)=(ON)/(LM)`
`=>25/10=y/16=45/x`
`=>y/16=45/x=5/2`
Với `y/16=5/2=>y=(16.5)/2=40`
Với `45/x=5/2=>x=(45.2)/5=18`
`3).`
Ta có: `ST \bot PQ` và `RP \bot PQ`
`=>ST //// RP`
Có: `QR=QS+SR=5+3,5=8,5`
`(QT)/(QP)=(QS)/(QR)`
`=>4/y=5/(8,5)`
`=>y=(4.8,5)/5`
`=>y=6,8`
`@Nae`

Một số cách chứng minh định lí Pitago Cách 1: Chứng minh của E. A. CoolidgeCách chứng minh này xuất hiện trong cuốn sách về các vấn đề kinh điển thuộc học thuyết Pitago của tác giả Elisha Scott Loomis, được xuất bản lần đầu tiên bởi Hội đồng giáo viên quốc gia của môn toán học, vào năm 1927. Thật đáng tiếc, quyển sách này hiện nay không được xuất bản nữa, trong cuốn sách này có tới trên 300 cách chứng minh định lý Pitago, trong đó, có nhiều cách chứng minh tương tự nhau, và tất cả các cách chứng minh nổi tiếng đều có trong cuốn sách của Loomis.Cách chứng minh dưới đây thì tương tự như cách chứng minh của Bhaskara trong phần “Behold!” đã giới thiệu ở bài trước. Cách chứng minh này được đăng trên tạp trí giáo dục, xuất bản hàng ngày, và tác giả của nó là cô E. A. Coolidge - là một người mù.Dựng hình và kiểm tra1. Vẽ một tam giác vuông và các hình vuông trên các cạnh của nó (dùng công cụ custom)2. Kéo dài tia HA, lấy điểm A’ đối xứng với điểm H qua A bằng cách :+ Chọn đoạn HA và điểm A+ Chọn menu Transform --> Rotate --> degrees =1803. Vẽ một đường thẳng đi qua điểm B và vuông góc với đoạn AA’, Vẽ điểm giao K của 2 đường này.( Hình bên minh họa cho các bước từ 1 đến 3)4. Vẽ hình vuông A’KLM.(Sử dụng công cụ Custom tool như đã giới thiệu ở bài 1)5. Vẽ Đoạn BK, GM, FL.6. Làm ẩn đi đường BK.7. Tô màu cho 4 mảnh trong hình vuông trên cạnh huyền.8. Đánh dấu vectơ EJ và dịch chuyển 4 đỉnh và 4 cạnh của hình vuông BCDE theo vectơ này (để được hình vuông bên dưới hình vuông trên cạnh b có diện tích bằng diện tích hình vuông BCDE )+ Đánh dấu theo thứ tự điểm E, J+ Chọn menu Transform --> Mark vector+ Đánh dấu 4 cạnh và 4 đỉnh của hình vuông BCDE+ Chọn vào Menu Transform --> Translate
Xem nội dung đầy đủ tại:http://123doc.org/document/542584-mot-so-cach-chung-minh-dinh-ly-pitago.htm
Có 6 cách nè:
Cách 1+cách 2:có trong SGK toán 7(PP diện tích)
Cách 3:(của một Tổng thống Mỹ hẳn hoi,ko biết có đúng ko)
Cho 2 tam giác vuông ABC và A'BC' (góc A= góc A' =90 độ)đặt cạnh nhau sao cho có được hình thang vuông ACC'A'(AC song song A'C') rồi dùng Đại số là ra
Cách 4:(của một nhà toán học Ấn Độ)
Dựng hình vuông ABCD và các tam giác vuông MAB,NBC,PCD,QDA để được hình vuông MNPQ rồi lại Đại số là ra
Cách 5:(thuần túy Hình học)Với ABC(góc A=90 độ) dựng ra ngoài 3 hình vuông ABDE,ACGH và BCM rồi dùng tam giác bằng nhau
Cách 6:Sử dụng hệ thức lượng trong tam giác vuông(lớp 9)

Ta có \(\sqrt{ab}=\sqrt{a}.\sqrt{b}\)
\(\Leftrightarrow\left(\sqrt{ab}\right)^2=\left(\sqrt{a}.\sqrt{b}\right)^2\)
\(\Leftrightarrow ab=\sqrt{a}^2.\sqrt{b}^2\)
\(\Leftrightarrow ab=a.b\)(luôn đúng)
Vậy ........

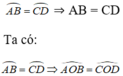
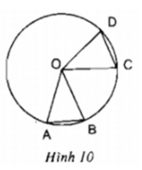
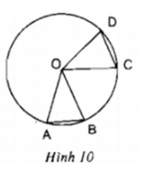
Xét ΔOAB và ΔOCD có:
OA = OC = R
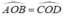
OB = OD = R
⇒ ΔOAB = ΔOCD (c.g.c)
⇒ AB = CD ( hai cạnh tương ứng)
AB = CD ⇒ 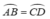
Xét ΔOAB và ΔOCD có:
OA = OC = R
AB = CD (gt)
OB = OD = R
⇒ ΔOAB = ΔOCD (c.c.c)
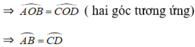

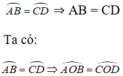
Xét ΔOAB và ΔOCD có:
OA = OC = R
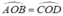
OB = OD = R
⇒ ΔOAB = ΔOCD (c.g.c)
⇒ AB = CD ( hai cạnh tương ứng)
b) AB = CD ⇒ 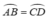
Xét ΔOAB và ΔOCD có:
OA = OC = R
AB = CD (gt)
OB = OD = R
⇒ ΔOAB = ΔOCD (c.c.c)
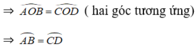

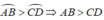
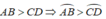
what ?
Tam giác ABC có MN // BC (M thuộc AB, N thuộc AC)
S(ACM)/S(ABC) = AM/AB (1)
S(ABN)/S(ABC) = AN/AC (2)
Mà S(ACM) = S(AMN) + S(CMN) (3)
và S(ABN) = S(AMN) + SBMN) (4)
Mặt khác do MNCB hình thang nên dễ dàng chứng minh
S(CMN) = S(BMN) (5)
Từ (3) , (4) và (5) cho:
S(ACM) = S(ABN) (6)
(1) , (2) và (6) cho:
AM/AB = AN/AC (đpcm)
-----------
Cách viết S(ABC) đọc là diện tích tam giác ABC