Cho x^2 + (m+1)x + m-1 =0 Tìm m để x1+x2=2024 Giúp với ạ.

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Phương Linh

9 tháng 4 2024 - olm

Cho x^2 + (m+1)x + m-1 =0

Tìm m để x1+x2=2024

Giúp với ạ.

#Toán lớp 9

Nguyễn Thị Thương Hoài

Giáo viên VIP

9 tháng 4 2024

Đúng(3)

Nguyễn Thị Thương Hoài

Giáo viên VIP

9 tháng 4 2024

Đúng(1)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Lê Hải Vy

18 tháng 7 2016 - olm

Cho phương trình (m-1)x^2 - 2.(2m+1)x + 4m+1 = 0

Tìm m để phương trình có hai nghiệm x1,x2 thỏa x1^2 + x2^2 = 1

Giúp mình với ạ!

#Toán lớp 9

Trần Thị Thủy Tiên

18 tháng 7 2016 - olm

Cho phương trình (m-1)x^2 - 2.(2m+1)x + 4m+1 = 0

Tìm m để phương trình có hai nghiệm x1,x2 thỏa x1^2 + x2^2 = 1

Giúp mình với ạ!

#Toán lớp 9

Trần Thị Thủy Tiên

18 tháng 7 2016

giúp mình

Đúng(0)

Phạm Tuân

18 tháng 8 2019 - olm

Bài 1 cho pt x^2-2(m+1)x+4m+m^2=0 .Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 sao cho biểu thức A =|x1-x2| đạt giá trị nhỏ nhất

bài 2 cho pt x^2+mx+2m-4=0.Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+|x2|=3

bài 3 cho pt x^2-3x-m^2+1=0.tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+2|x2|=3

#Toán lớp 9

nguyen abc

26 tháng 2 2017 - olm

Giúp mình với đang cần gấp !! Cho pt x^2 - 2(m - 1) x + m^2 = 0 . Tìm m để pt có 2 nghiệm x1 , x2 thỏa mãn ( x1 - m)^2 + x2 = m + 2.Dang can giup ! Rang nha

#Toán lớp 9

Mai Thisim

3 tháng 5 2017 - olm

Cho x² - 2(m+1)x + m² +2 = 0

Với giá trị nào của m để pt có 2 nghiệm x1, x2. Tìm m để 3x1-x2 =0

#Toán lớp 9

Lê Thụy Sĩ

20 tháng 5 2019 - olm

Cho phương trình: \(x^2-2\left(m-1\right)x+m^2-3m=0;\) ( có ẩn số x).

a) Tìm m để phương trình có hai nghiệm phân biệt x1 và x2.

b) Tìm m để biểu thức \(T=x1^2+x2^2-\left(m-1\right)\left(x1+x2\right)+m^2-3m\)đạt giá trị nhỏ nhất .

AI GIẢI VỚI Ạ NHANH GIÙM HUHU !!!!

#Toán lớp 9

Phùng Minh Quân

20 tháng 5 2019

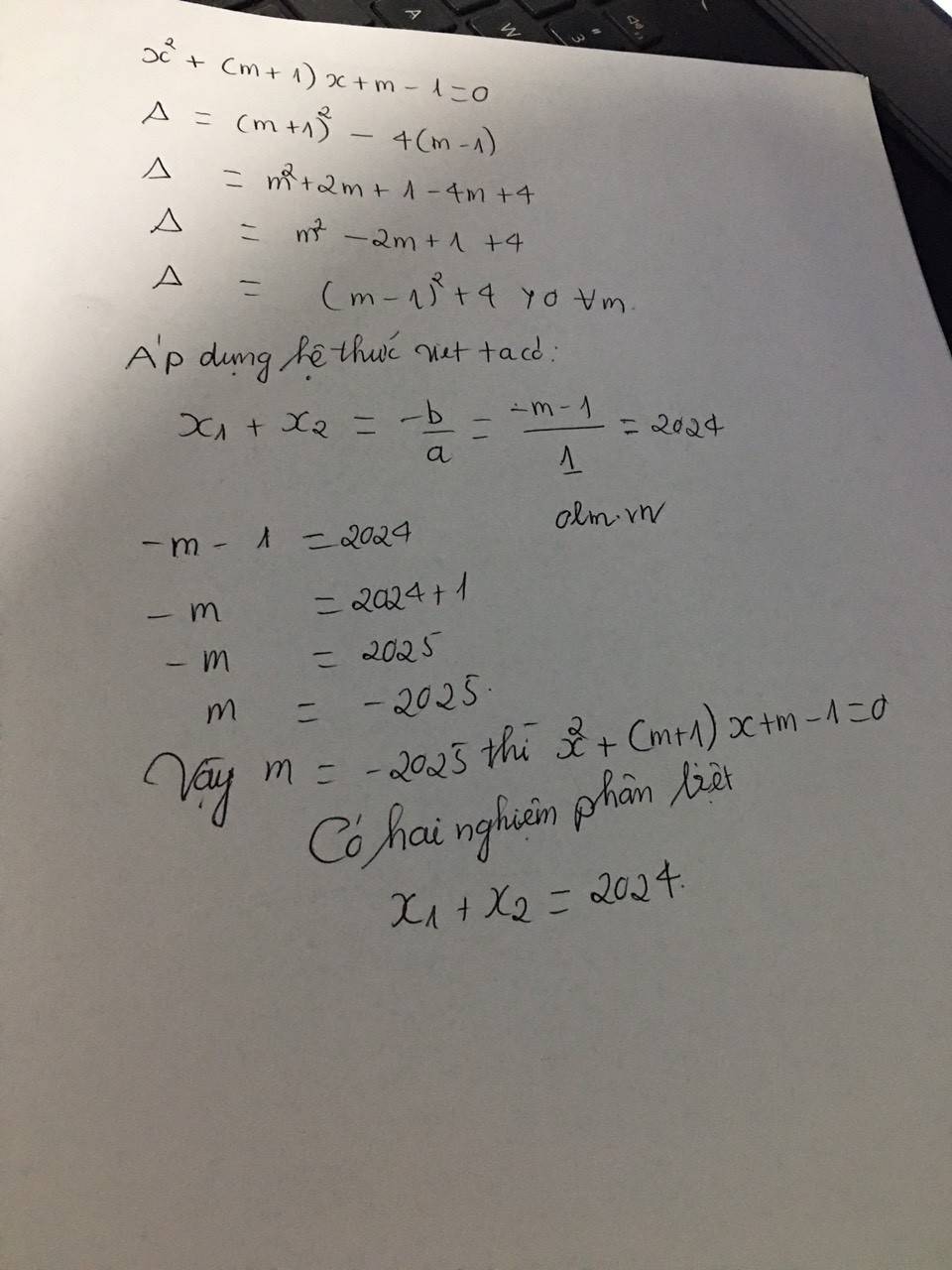
\(a)\) Để pt có hai nghiệm phân biệt \(x_1,x_2\) thì \(\Delta'=\left(1-m\right)^2-m^2+3m=1-2m+m^2-m^2+3m=m+1>0\)\(\Leftrightarrow\)\(m>-1\)

Vậy để pt có hai nghiệm phân biệt \(x_1,x_2\) thì \(m>-1\)

\(b)\) Ta có : \(T=x_1^2+x_2^2-\left(m-1\right)\left(x_1+x_2\right)+m^2-3m\)

\(T=\left(x_1+x_2\right)^2-2x_1x_2+\left(1-m\right)\left(x_1+x_2\right)+m^2-3m\)

Theo định lý Vi-et ta có : \(\hept{\begin{cases}x_1+x_2=2\left(1-m\right)\\x_1x_2=m^2-3m\end{cases}}\)

\(\Rightarrow\)\(T=4\left(1-m\right)^2-2\left(m^2-3m\right)-2\left(1-m\right)\left(1-m\right)+m^2-3m\)

\(T=4m^2-8m+4-2m^2+6m-2m^2+4m-2+m^2-3m\)

\(T=m^2-m+2=\left(m^2-m+\frac{1}{4}\right)+\frac{7}{4}=\left(m-\frac{1}{2}\right)^2+\frac{7}{4}\ge\frac{7}{4}\)

Dấu "=" xảy ra \(\Leftrightarrow\)\(m=\frac{1}{2}\) ( thoả mãn )

Vậy GTNN của \(T=\frac{7}{4}\) khi \(m=\frac{1}{2}\)

Đúng(0)

Phùng Bảo Trân

10 tháng 7 2020 - olm

Cho phương trình bậc hai x^2 - 2(m-1)x + m^2 + m + 1=0 (m là tham số). Tìm tất cả các giá trị của m để phương trình có hai nghiệm x1, x2 thõa mãn x1^2 + x2^2 = 4x1x2 - 2

Các bạn giúp mình với !

#Toán lớp 9

๖²⁴ʱんuﾘｲú❄✎﹏

10 tháng 7 2020

Ta có : \(x^2-2\left(m-1\right)x+m^2+m+1=0\left(a=1;b=-2m+2;c=m^2+m+1\right)\)

\(\Delta=\left(-2m+2\right)^2-4\left(m^2+m+1\right)=4m^2+4-4m^2-4m-4=-4m< 0\)

Nếu \(-4m< 0\Leftrightarrow m>0\) chắc ĐK là vậy.

Theo hệ thức Vi et ta có : \(x_1+x_2=2m+2;x_1x_2=m^2+m+1\)

Theo bài ra ta có : \(x_1^2+x_2^2=4x_1x_2-2\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=4x_1x_2-2\) Thay vao ta có pt mới :

\(\Leftrightarrow\left(2m+2\right)^2-4\left(m^2+m+1\right)=4\left(m^2+m+1\right)-2\)

\(\Leftrightarrow4m+4-4m^2-m-1=4m^2+4m+4-2\)

\(\Leftrightarrow3m+3-4m^2=4m^2+4m+2\)

\(\Leftrightarrow-m+1-8m^2=0\) Ta có : \(\left(-1\right)^2-4\left(-8\right)=1+32=33>0\)

\(x_1=\frac{1-\sqrt{33}}{-16};x_2=\frac{1+\sqrt{33}}{-16}\)

Đúng(0)

๖²⁴ʱんuﾘｲú❄✎﹏

10 tháng 7 2020

Tớ ngu ! tớ nhận.

Sửa từ dòng 4 trở lên.

\(\Leftrightarrow4m^2+4-4m^2-m-1=4m^2+4m+4-2\)

\(\Leftrightarrow3-m=4m^2+4m+2\)

\(\Leftrightarrow3-m-4m^2-4m-2=0\)

\(\Leftrightarrow1-5m-4m^2=0\)Ta có : \(\left(-5\right)^2-4\left(-4\right)=25+16=41>0\)

\(x_1=\frac{5-\sqrt{41}}{-4};x_2=\frac{5+\sqrt{41}}{-4}\)

Đúng(0)

Bắc Hạnh

20 tháng 5 2016

Cho pt X^2 -2(m-1)x+m+1=0

Giải pt khi m=1 và tìm m để pt có 2 nghiệm x1,x2 thoả mãn x1/x2 +x2/x1 =4

#Toán lớp 9

Ngọc Vĩ

20 tháng 5 2016

a/ Thay m = 1 vào pt ta được: x² + 2 = 0 => x² = -2 => pt vô nghiệm

b/ Theo Vi-ét ta được: \(\begin{cases}x_1+x_2=2m-2\\x_1.x_2=m+1\end{cases}\)

\(\frac{x_1}{x_2}+\frac{x_2}{x_1}=4\) \(\Leftrightarrow\frac{x_1^2+x_2^2}{x_1x_2}=4\) \(\Leftrightarrow\frac{\left(x_1+x_2\right)^2-2x_1x_2}{x_1x_2}=4\) \(\Leftrightarrow\frac{\left(2m-2\right)^2-2\left(m+1\right)}{m+1}=4\) \(\Leftrightarrow\frac{4m^2-8m+4-2m-2}{m+1}=4\) \(\Leftrightarrow4m^2-10m+2=4m+4\) \(\Leftrightarrow4m^2-14m-2=0\)

Giải denta ra ta được 2 nghiệm: \(\begin{cases}x_1=\frac{7+\sqrt{57}}{4}\\x_2=\frac{7-\sqrt{57}}{4}\end{cases}\)

Đúng(0)

Hồng Trinh

20 tháng 5 2016

Khi m=1 ta có : \(x^2-2=0\Leftrightarrow x=\pm\sqrt{2}\)

Pt 2 nghiệm x₁ ; x₂ thỏa mãn : \(\frac{x_1}{x_2}+\frac{x_2}{x_1}=4\) \(\Leftrightarrow\frac{x_1^2+x_2^2}{x_1+x_2}=4\Leftrightarrow\frac{x_1^2+x_2^2-2x_1x_2+2x_1x_2}{x_1+x_2}=4\) \(\Leftrightarrow\frac{\left(x_1+x_2\right)^2-2x_1x_2}{x_1+x_2}=4\) (1)

Theo viet ta có: \(x_1x_2=\frac{c}{a}=\left(m+1\right)\); \(x_1+x_2=\frac{-b}{a}=2\left(m+1\right)\)

Thay vài (1) ta có: \(\frac{\left[2\left(m+1\right)\right]^2-2\left(m-1\right)}{2\left(m+1\right)}=4\) \(\Leftrightarrow4\left(m^2+2m+1\right)-2m+1=8\left(m+1\right)\Leftrightarrow4m^2+6m+5-8m-8=0\) \(\Leftrightarrow4m^2-2m-3=0\Leftrightarrow\left[\begin{array}{nghiempt}m=\frac{1+\sqrt{13}}{4}\\m=\frac{1-\sqrt{13}}{4}\end{array}\right.\)

Đúng(0)

Dương Thị Tường VI

30 tháng 4 2019 - olm

cho pt x^2-2(m+1)x+2m=0

a, GPT khi m=1

b, tìm m để pt có 2 nghiệm x1, x2 thoãn mãn hệ thức căn x1+căn x2=căn2

giúp hộ mk vs

#Toán lớp 9

Lê Ng Hải Anh

30 tháng 4 2019

Phần a dễ bạn tự làm nha!!! :))

b, Ta có: \(\Delta^'=\left[-\left(m+1\right)\right]^2-2m=m^2+2m+1-2m=m^2+1>0\forall m\)

=> PT luôn có 2 nghiệm phân biệt

Theo Vi-ét, ta có: \(\hept{\begin{cases}x_1+x_2=2\left(m+1\right)\\x_1x_2=2m\end{cases}}\)

Ta có: \(\sqrt{x_1}+\sqrt{x_2}=\sqrt{2}\)

\(\Leftrightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=2\)

\(\Leftrightarrow x_1+2\sqrt{x_1x_2}+x_2=2\)

\(\Leftrightarrow x_1+x_2-2+2\sqrt{x_1x_2}=0\)

\(\Leftrightarrow2\left(m+1\right)-2+2\sqrt{2m}=0\)

\(\Leftrightarrow2m+2\sqrt{2m}=0\)

\(\Leftrightarrow m+\sqrt{2m}=0\)

\(\Leftrightarrow\sqrt{m}\left(\sqrt{m}+\sqrt{2}\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}\sqrt{m}=0\\\sqrt{m}+\sqrt{2}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}m=0\\\sqrt{m}=-\sqrt{2}\end{cases}}}\)

Vậy: m = 0

=.= hk tốt!!

Đúng(0)

Lê Hồ Trọng Tín

30 tháng 4 2019

a) Khi m=1 thì pt<=>x²-4x+2=0

Có:\(\Delta\)'=(-2)^2-2=2>0=>pt có 2 nghiệm là x₁=\(2+\sqrt{2}\)và x₂=2-\(\sqrt{2}\)

b)Để pt có nghiệm thì \(\Delta\)'=(m+1)²-2\(\ge\)0<=>m\(\ge\)\(\sqrt{2}\)-1

Theo định lý Viète thì:x₁+x₂=2(m+1)=\(\sqrt{2}\)<=>\(\frac{\sqrt{2}-2}{2}\)

Đúng(0)

Tiên Tiên

22 tháng 7 2015 - olm

Các bạn ơi giúp mình bài này nhé.

Cho pt x2+2(m-1)x-2m+5=0

Tìm m để a) pt (1) có 2 no x1,x2 tm x1/x2 + x2/x1=2

b) pt (1) có 2 no x1,x2 tm 2x1+3x2=5

#Toán lớp 9

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP