Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta thấy tam giác AEH và ADH đều là các tam giác vuông chung cạnh huyền AH nên AEHD nội tiếp đường tròn đường kính AH.
b) Gọi O là trung điểm của AH và K là giao điểm của AH với BC. Do H là trực tâm nên ta có ngay AK là đường cao của tam giác ABC.
Theo tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông ta có:
^OEH=^OHE=^KHC; ^MEC=^MCE.
mà ^KHC+^MCE=90o.
Suy ra: ^OEH+^MEC=90o nên OE⊥EM hay ME tiếp xúc với đường tròn ngoại tiếp tứ giác AEHD.

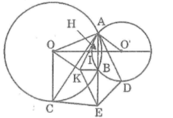
Vì AB ⊥ KB nên AE ⊥ KB
Lại có: AB = BE (tính chất đối xứng tâm)
Suy ra: KA = KE (tính chất đường trung trực) (3)
Ta có: IO = IO’ (gt)
IA = IK (chứng minh trên)
Tứ giác AOKO’ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Suy ra: OK // O’A và OA // O’K
CA ⊥ O’A (vì CA là tiếp tuyến của đường tròn (O’))
OK // O’A (chứng minh trên)
Suy ra: OK ⊥ AC
Khi đó OK là đường trung trực của AC
Suy ra: KA = KC (tính chất đường trung trực) (4)
DA ⊥ OA (vì DA là tiếp tuyến của đường tròn (O))
O’K // OA (chứng minh trên)
Suy ra: O’K ⊥ DA
Khi đó O’K là đường trung trực của AD
Suy ra: KA = KD (tính chất đường trung trực) (5)
Từ (3), (4) và (5) suy ra: KA = KC = KE = KD
Vậy bốn điểm A, C, E, D cùng nằm trên một đường tròn.3

Lời giải:
a)
Dễ thấy \(IA=IB=R(I); KA=KB=R(K)\) nên tam giác \(IAB; KAC\) là tam giác cân.
Áp dụng tính chất tam giác cân và tính chất tiếp tuyến: \(\widehat{IAB}=\widehat{IBA}=\widehat{IBC}-\widehat{ABC}=90^0-\widehat{ABC}\)
\(\widehat{KAC}=\widehat{KCA}=\widehat{KCB}-\widehat{ACB}=90^0-\widehat{ACB}\)
\(\Rightarrow \widehat{IAB}+\widehat{KAC}=180^0-(\widehat{ABC}+\widehat{ACB})\)
\(\Leftrightarrow \widehat{IAB}+\widehat{KAC}=180^0-90^0=90^0\)
\(\Leftrightarrow \widehat{IAK}=90^0+\widehat{BAC}=90^0+90^0=180^0\)
\(\Rightarrow I,A,K\) thẳng hàng.
Hai đường tròn (I); (K) giao nhau tại A và I,A,K thẳng hàng nên IA+AK=IK nên (I) và (K) tiếp xúc với nhau tại A.
b)
Tam giác BAC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền nên \(AM=\frac{BC}{2}=BM\Rightarrow \triangle MAB\) cân tại M
\(\Rightarrow \widehat{MAB}=\widehat{MBA}=\widehat{CBA}=90^0-\widehat{IBA}=90^0-\widehat{IAB}\)
\(\Rightarrow \widehat{IAM}=\widehat{MAB}+\widehat{IAB}=90^0\Rightarrow IA\perp AM\) nên AM là tiếp tuyến của (I)
Hoàn toàn tương tự ta có AM là tiếp tuyến của (K)
Ta có đpcm.

A B C O M N E K T
a) Có ^AOB = 1800 - ^OAB - ^OBA = 1800 - ^BAC/2 - ^ABC/2 = 900 + (1800 - ^BAC - ^ABC)/2 = 900 + ^ACB/2
b) Dễ thấy A,M,O,E cùng thuộc đường tròn đường kính OA (Vì ^AMO = ^AEO = 900) (1)
Ta có ^AOK = 1800 - ^AOB = 1800 - (900 + ^ABC/2) = 900 - ^ACB/2 = ^CEN (Do \(\Delta\)CEN cân tại C)
=> Tứ giác AOKE nội tiếp hay A,O,K,E cùng thuộc một đường tròn (2)
Từ (1) và (2) suy ra năm điểm A,M,K,O,E cùng thuộc một đường tròn (đpcm).
c) Ta thấy A,O,K,E cùng thuộc một đường tròn (cmt) và OK cắt AE tại T
Nên \(\frac{KT}{ET}=\frac{AT}{OT}\)(Hệ thức lượng đường tròn). Kết hợp \(\frac{AT}{OT}=\frac{AB}{OB}\)(AO là phân giác ^BAT)
Suy ra \(\frac{KT}{ET}=\frac{AB}{OB}\). Mặt khác: ^BKN = ^OAE = ^BAO và ^NBK = ^OBA => \(\Delta\)BKN ~ \(\Delta\)BAO (g.g)
=> \(\frac{AB}{OB}=\frac{KB}{NB}\). Từ đây \(\frac{KT}{ET}=\frac{KB}{BN}\)=> KT.BN = KB.ET (đpcm).

(Bởi vì CM trực tiếp hơi khó nên mình CM bằng trùng hình)
Vẽ \(AM\) là trung tuyến của tam giác \(ABC\) và tia \(AE\) thoả \(\widehat{BAE}=\widehat{CAM}\) (trong đó \(E\in\left(O\right)\)). Gọi \(D',N\) lần lượt là trung điểm của \(AE,AC\).
-----
Bước 1: CM: \(\widehat{AD'O}=90^o\) (hiển nhiên).
Bước 2: CM \(D\) trùng với \(D'\).
Tam giác \(ABE\) và \(AMC\) đồng dạng (g.g) nên tam giác phân bởi đường trung tuyến cũng đồng dạng.
Cụ thể là tam giác \(ABD'\) và \(AMN\) đồng dạng.
Suy ra \(\widehat{ABD'}=\widehat{AMN}=\widehat{BAM}\) (so le trong, \(MN\) song song \(AB\)).
Mà \(\widehat{BAM}=\widehat{EAC}\) nên \(\widehat{ABD'}=\widehat{D'AC}\).
Từ đó suy ra \(AC\) tiếp xúc với đường tròn ngoại tiếp \(ABD'\).
Tương tự suy ra \(AB\) tiếp xúc với đường tròn ngoại tiếp \(ACD'\).
Vậy \(D\) trùng với \(D'\) và ta có đpcm.


A C B D O M S T L K E F
Nhận xét: Tứ giác ABCD nội tiếp đường tròn đường kính AC vì ^ABC=^CDA=900. Gọi tâm của đường tròn này là O. Khi đó thì O chính là trung điểm đoạn AC. Ta thấy M là 1 điểm chung của (S) và (T), đồng thời là trung điểm BD nên M nằm trên trung trực BD. Gọi giao điểm thứ hai của (S) và (T) là L. Ta đi chứng minh L cũng nằm trên trung trực BD. Thật vậy:
Từ M kẻ MK vuông góc với đường thẳng ST. Gọi E,F lần lượt là hình chiếu của S,T lên MA,MC.
Khi đó các tứ giác KSEM, KTMS nội tiếp => ^EKF = ^MKE + ^MKF = ^MSE + ^MTF = (^ASM + ^CTM)/2
Ta thấy AC là tiếp tuyến chung của (S) và (T) nên ^MAC = ^ASM/2; ^MCA = ^CTM/2
Từ đó: ^EKF = ^MCA + ^MAC = ^EOA + ^FOC (Chú ý tứ giác MEOF là hbh) = 1800 - ^EOF
Suy ra tứ giác KEOF nội tiếp => ^EKO = ^EFO = ^MAC = ^MSE (=^ASM/2) = ^EKM
Mà M và O nằm cùng phía so với EK nên tia KM,KO trùng nhau hay O,M,K thẳng hàng
Mặt khác: (S) và (T) cắt nhau tại M và L nên ML vuông góc ST. Do MK vuông góc ST nên M,K,L thẳng hàng
Vì vậy 4 điểm O,M,K,L thẳng hàng. Lại có OM là trung trực của BD => ML cũng là trung trực BD
Hay 2 giao điểm của (S) và (T) cùng nằm trên đường trung trực của BD (đpcm).