Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt AB = a; BC = b; CD = c; AD = d
C A B 2 = 2 π . a 2 2 = π . a 2 . Tương tự C C D 2 = π . c 2
Vậy C A B 2 + C C D 2 = π 2 a + c
Có C B C 2 + C C D 2 = π 2 b + d
Tứ giác ABCD ngoại tiếp, kết hợp tính chất tiếp => a + c = b + d => ĐPCM

Ta có : A là giao điểm của 2 đường tiếp tuyến tại E và G của O =>AG=AE
Chứng minh tương tự,ta được BE=BH
=>AG+BH=AB
Tương tự,ta có DG+HC=CD
=>AB+CD=AD+BC=10cm
nửa đường tròn tâm G: 2AG.π/2=AG.π=1/2.AD.π
nửa đường tròn tâm H:1/2.BC.π
=> S=1/2(AD+BC)π=5π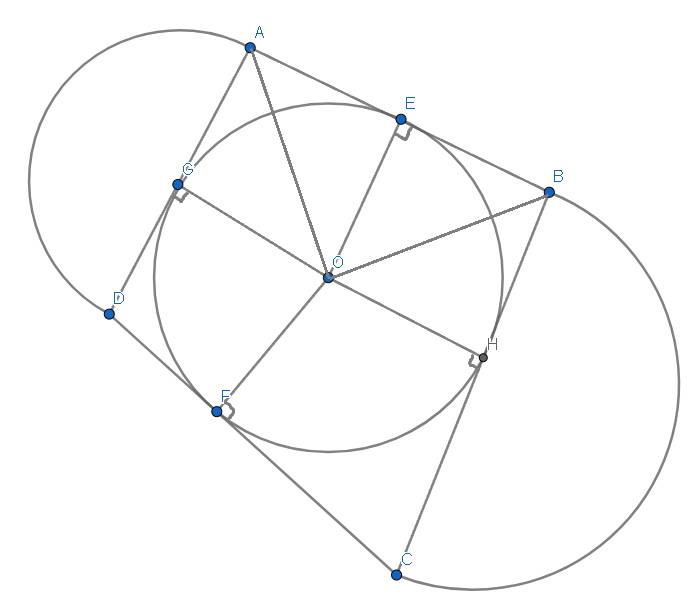

a, Chứng minh được DBOF nội tiếp đường tròn tâm I là trung điểm của DO
b, O A = O F 2 + A F 2 = 5 R 3 => cos D A B ^ = A F A O = 4 5
c, ∆AMO:∆ADB(g.g) => D M A M = O B O A
mà M O D ^ = O D B ^ = O D M ^ => DM = OM
=> D B D M = D B O M = A D A M . Xét vế trái B D D M - D M A M = A D - D M A M = 1
d, D B = A B . tan D A B ^ = 8 R 3 . 3 4 = 2 R => O M = A O . tan D A B ^ = 5 R 4
=> S O M D B = 13 R 2 8
S O M D B ngoài = S O M D B - 1 4 S O , R = R 2 8 13 - 2 π

c) Gọi giao điểm của BM với Ax là I. Từ M kẻ MK vuông góc với AB. BC cắt MK tại E.
Vì MK vuông góc AB => MK // AC // BD
EK // AC => \(\frac{EK}{AC}=\frac{BE}{BC}\); ME // IC => \(\frac{ME}{IC}=\frac{BE}{BC}\) => \(\frac{EK}{AC}=\frac{ME}{IC}\)
Tam giác MIA vuông tại M có CA = CM => góc CAM = góc CMA => góc CIM = góc CMI => tam giác CMI cân tại C => CI = CM => CM = CI = CA => EK = ME.
\(EK=ME\Rightarrow\frac{EK}{BD}=\frac{ME}{BD}\)mà \(\frac{ME}{BD}=\frac{CM}{CD}=\frac{AK}{AB}\Rightarrow\frac{EK}{BD}=\frac{AK}{AB}\)
=> Tam giác AKE đồng dạng với tam giác ABD (c.g.c) => góc EAK = góc DAK => A,E,D thẳng hàng => BC cắt AD tại E mà theo giả thiết BC cắt AD tại N => E trùng với N => H trùng với K => N là trung điểm MH.