Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt AB = a; BC = b; CD = c; AD = d
C A B 2 = 2 π . a 2 2 = π . a 2 . Tương tự C C D 2 = π . c 2
Vậy C A B 2 + C C D 2 = π 2 a + c
Có C B C 2 + C C D 2 = π 2 b + d
Tứ giác ABCD ngoại tiếp, kết hợp tính chất tiếp => a + c = b + d => ĐPCM

a) Chứng minh tứ giác OBDF nội tiếp.
Định tâm I đường tròn ngoại tiếp tứ OBDF.
Ta có: DBO = 900 và DFO = 900(tính chất tiếp tuyến)
Tứ giác OBDF có DBO+DFO =1800 nên nội tiếp được trong một đường tròn.
Tâm I đường tròn ngoại tiếp tứ giác OBDF là trung điểm của OD
b) Tính Cos DAB .
Áp dụng định lí Pi-ta-go cho tam giác OFA vuông ở F ta được:
\(OA=\sqrt{OF^2+AF^2}=\sqrt{R^2+\left(\frac{4R}{3}\right)}=\frac{5R}{3}\)
\(COS\)\(FAO=\frac{AF}{OA}=\frac{4R}{3}:\frac{5R}{3}=0,8=>COSDAB=0,8\)
c) Kẻ OM ⊥ BC ( M ∈ AD) . Chứng minh \(\frac{BD}{DM}-\frac{DM}{AM}\) =1
∗ OM // BD ( cùng vuông góc BC) ⇒ MOD BDO = (so le trong) và BDO ODM = (tính chất hai tiếp tuyến cắt nhau)
Suy ra: MDO =MOD.
Vậy tam giác MDO cân ở M. Do đó: MD = MO
∗ Áp dụng hệ quả định lí Ta let vào tam giác ABD có OM // BD ta được:
\(\frac{BD}{OM}=\frac{AD}{AM}HAY\frac{BD}{DM}=\frac{AD}{AM}\)(VÌ MD=MO)
\(=>\frac{BD}{DM}=\frac{AM+DM}{AM}=1+\frac{DM}{AM}\)
Do đó:\(\frac{DM}{BM}-\frac{DM}{AM}=1\left(đpcm\right)\)
d) Tính diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường tròn (O) theo R.
∗Áp dụng hệ thức lượng cho tam giác OAM vuông ở O có OF ⊥ AM ta được:
OF2 = MF. AF hay R2 = MF. \(\frac{4r}{3}\)⇒ MF = \(\frac{3r}{4}\)
∗ Áp dụng định lí pi ta go cho tam giác MFO vuông tại F ta được:
OM = \(\sqrt{OF^2+MF^2}=\sqrt{R^2+\frac{3R}{4}^2}=\frac{5R}{4}\)
∗ OM //BD =>\(\frac{OM}{BD}=\frac{AO}{AB}=>BD=\frac{OM.AB}{OA}=\frac{5R}{4}.\left(\frac{5R}{3}+R\right):\frac{5R}{3}=2R\)
Gọi S là diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường tròn (O)
S1 là diện tích hình thang OBDM.
S2 là diện tích hình quạt góc ở tâm BON = 90 0
Ta có: S = S1 – S2 .
\(S1=\frac{1}{2}\left(OM+BD\right).OB=\frac{1}{2}\left(\frac{5R}{4}+2R\right).R=\frac{13R^2}{8}\left(đvdt\right)\)
\(S2=\frac{\pi R^2.90^0}{360^0}=\frac{\pi R^2}{4}\left(đvdt\right)\)
Vậys=s1-s2=\(\frac{13r^2}{8}-\frac{\pi r^2}{4}=\frac{r^2}{8}\left(13-2\pi\right)\left(đvdt\right)\)

A B O C D K H E
Nhận xét: tam giác OAD = OBC (Vì OA = OB ; OD = OC; AD = BC = 2\(\sqrt{5}\))
=> S DAO = SCBO mà 2 đáy OA = OB
=> đường cao DK = CH
Dễ dang => CD // AB do đó, CH = DK = OE
Gọi bán kính đtr = R
Xét tam giác vuông OED có: OE2 = R2 - 32 = R2 - 9
=> DK2 = R2 - 9
+) Mặt khác, dễ có: CD = HK và OH = OK
=> OK = HK/ 2 = 6/2 = 3cm
=> AK = R - 3 (cm)
+) Xét tam giác vuông AKD có: DK2 + AK2 = AD2
=> R2 - 9 + (R - 3)2 = (2\(\sqrt{5}\))2
=> 2.R2 - 6R = 20
=> R2 - 3R - 10 = 0
<=> R2 - 5R + 2R - 10 = 0
<=> (R - 5)(R + 2) = 0 => R = 5 hoặc R = -2 mà R > 0
Vậy R = 5cm
)

a) Xét (O) có :
AB là tiếp tuyến tại B
AC là tiếp tuyến tại C
AB cắt AC tại A
\(\Rightarrow\widehat{ABO}=\widehat{ACO}=90^o\)và OA là p/g \(\widehat{BOC}\)
Xét tg ABOC có \(\widehat{ABO}+\widehat{ACO}=180^o\)Mà 2 góc này đối nhau
\(\Rightarrow\)ABOC là tg nt
b) Xét (O) có
\(\widehat{ABE}\)là góc tạo bởi tiếp tuyến AB và dây BE
\(\widehat{BDE}\)là góc nt chắn cung BE
\(\Rightarrow\widehat{ABE}=\widehat{BDE}=\frac{1}{2}sđ\widebat{BE}\)
Xét \(\Delta ABEvà\Delta ADB:\)
\(\widehat{BAD}\)chung
\(\widehat{ABE}=\widehat{BDE}\)
\(\Rightarrow\Delta ABE\infty\Delta ADB\left(gg\right)\)
\(\Rightarrow\frac{AB}{AD}=\frac{AE}{AB}\Rightarrow AB^2=AD.AE\)
c) Vì OA là p/g \(\widehat{BOC}\Rightarrow\widehat{BOA}=\widehat{COA}=\frac{\widehat{BOC}}{2}\)
Do ABOC là tg nt\(\Rightarrow\widehat{BOA}=\widehat{BCA}\)(cùng chắn cung AB)
Suy ra \(\widehat{AOC}=\widehat{ACB}\)
 Phạm Cao Thúy An: Biết rồi còn hỏi làm gì?
Phạm Cao Thúy An: Biết rồi còn hỏi làm gì?
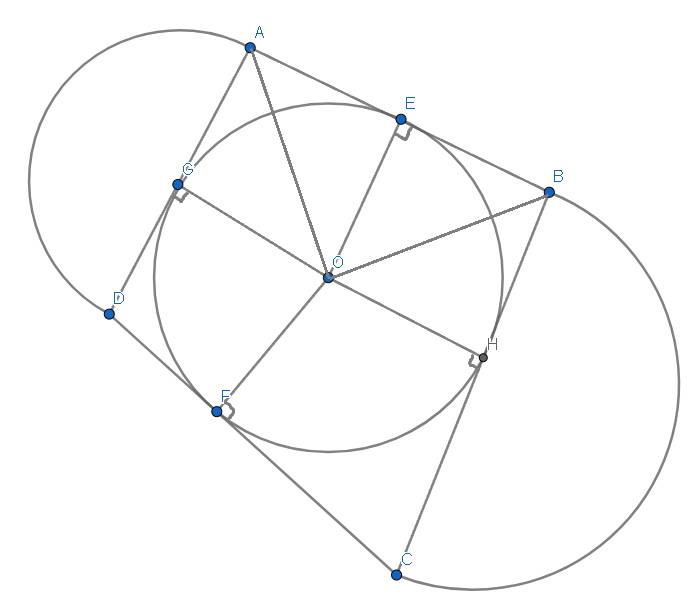
Ta có : A là giao điểm của 2 đường tiếp tuyến tại E và G của O =>AG=AE
Chứng minh tương tự,ta được BE=BH
=>AG+BH=AB
Tương tự,ta có DG+HC=CD
=>AB+CD=AD+BC=10cm
nửa đường tròn tâm G: 2AG.π/2=AG.π=1/2.AD.π
nửa đường tròn tâm H:1/2.BC.π
=> S=1/2(AD+BC)π=5π