Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

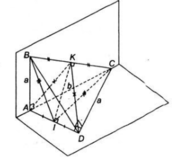


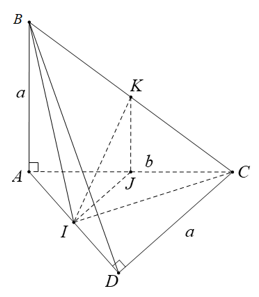
Chứng minh tương tự, ta có tam giác AKD là tam giác cân tại K có KI là đường trung tuyến nên đồng thời là đường cao.
⇒ IK ⊥ AD (2)
Từ (1) và (2) suy ra; IK là đường vuông góc chung của hai đường thẳng AD và BC.

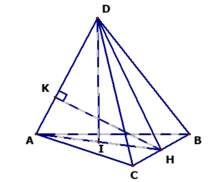
CMR: DI ⊥ (ABC).
● AD = a, DH = a ΔDAH cân tại D.
- Mặt khác I là trung điểm của AH nên DI ⊥ AH.
● BC ⊥ (ADH) ⇒ BC ⊥ DI.
⇒ DI ⊥ (ABC).

a.
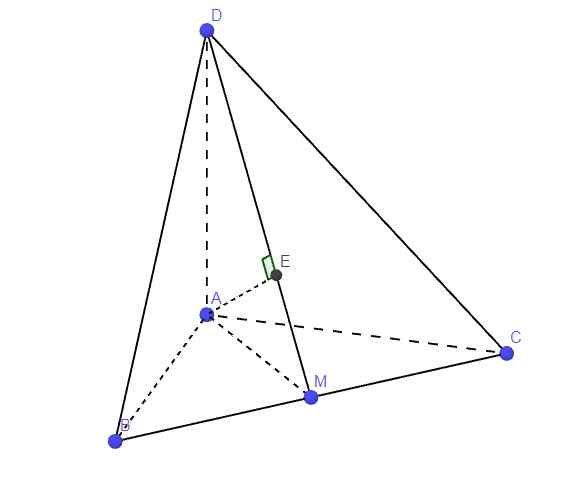
Do \(AB=AC\Rightarrow\Delta ABC\) cân tại A
\(\Rightarrow AM\) là trung tuyến đồng thời là đường cao
\(\Rightarrow AM\perp BC\) (1)
Mà \(\left\{{}\begin{matrix}AD\perp AB\left(gt\right)\\AD\perp AC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(ABC\right)\Rightarrow AD\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(ADM\right)\)
b.
Từ A kẻ \(AE\perp DM\) (E thuộc DM)
Do \(BC\perp\left(ADM\right)\Rightarrow BC\perp AE\)
\(\Rightarrow AE\perp\left(BCD\right)\Rightarrow AE=d\left(A;\left(BCD\right)\right)\)
\(BC=\sqrt{AB^2+AC^2}=5\sqrt{2}\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{5\sqrt{2}}{2}\)
Hệ thức lượng trong tam giác vuông ADM:
\(AE=\dfrac{AD.AM}{\sqrt{AD^2+AM^2}}=\dfrac{5\sqrt{3}}{3}\)
c.
Do \(AD\perp\left(ABC\right)\) theo cmt \(\Rightarrow AM\) là hình chiếu vuông góc của DM lên (ABC)
\(\Rightarrow\widehat{DMA}\) là góc giữa DM và (ABC)
\(tan\widehat{DMA}=\dfrac{AD}{AM}=\sqrt{2}\Rightarrow\widehat{DMA}\approx54^044'\)

Đáp án B
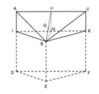 |
Góc giữa mặt phẳng (ABC) và (DEF) bằng với góc giữa 2 mặt phẳng (ABC) và (BIK) trong đó mặt phẳng (BIK) song song với (DEF)

Vẽ đường cao BH của tam giác đều ABC, suy ra H là trung điểm AC và BH = a 3 2
Gọi M là trung điểm IK. Khi đó HM là đường trung bình của hình chữ nhật AIKC
HM =AI = a 2 và HM song song với AI
![]()
Trong mặt phẳng (BHM) vẽ MG ⊥ BH tại G
Do MG ⊥ BH và AC ⊥ MG(AC ⊥ (BHM)) nên MG ⊥ (ABC) (2)
Từ (1) và (2) => góc giữa 2 mặt phẳng (ABC) và (BKI) bằng góc giữa MG với HM, tức góc HMG
Trong ∆ B H M vuông tại M, ta có:
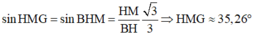

a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: BC vuông góc (SAM)
=>BC vuông góc SM
=>(SM;(ABC))=90 độ


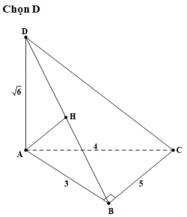
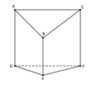
\(DA\perp\left(ABC\right)\Rightarrow AB\) là hình chiếu của BD lên (ABC)
\(\Rightarrow\widehat{DBA}\) là góc giữa BD và (ABC)
\(tan\widehat{DBA}=\frac{AD}{AB}=\sqrt{3}\Rightarrow\widehat{DBA}=60^0\)
Gọi H là trung điểm AC \(\Rightarrow BH\perp AC\) (tam giác cân thì trung tuyến tại đỉnh là đường cao)
\(AD\perp\left(ABC\right)\Rightarrow AD\perp BH\)
\(\Rightarrow BH\perp\left(ACD\right)\Rightarrow\widehat{BDH}\) là góc giữa BD và (DAC)
\(AC=AB\sqrt{2}=a\sqrt{2}\Rightarrow BH=\frac{AC}{2}=\frac{a\sqrt{2}}{2}\)
\(BD=\sqrt{AD^2+AB^2}=2a\)
\(\Rightarrow sin\widehat{BDH}=\frac{BH}{BD}=\frac{\sqrt{2}}{4}\Rightarrow\widehat{BDH}\approx20^042'\)