Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

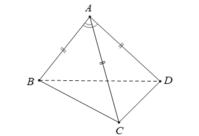
\(\left\{{}\begin{matrix}\widehat{BAC}=60^0\\AB=AC\end{matrix}\right.\) \(\Rightarrow\Delta ABC\) đều \(\Rightarrow AB=BC\)
Tương tự ta có \(\Delta ABD\) đều \(\Rightarrow BD=AB=BC\)
\(\Rightarrow\Delta ACD=\Delta BCD\left(c.c.c\right)\)
\(\Rightarrow AJ=BJ\) (cùng là trung tuyến của 2 tam giác bằng nhau)
\(\Rightarrow\Delta ABJ\) cân tại J
\(\Rightarrow IJ\perp AB\)
Dữ kiện \(\widehat{CAD}=90^0\) là ko cần thiết
P/s: quên vẽ hình

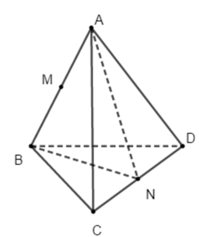
Các tam giác ABC và ABD là tam giác đều ⇒ tam giác ACD cân
⇒ BN ⊥ CD và AN ⊥ CD ⇒ góc ANB là góc của hai mặt phẳng (ACD) và (BCD)
Đáp án B

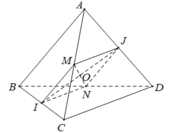
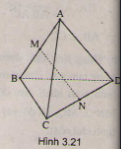
- Gọi M, N lần lượt là trung điểm AC, BC.
+) Tam giác ACD có MJ là đường trung bình của tam giác nên :
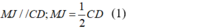
+) Tam giác BCD có NI là đường trung bình của tam giác nên:
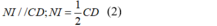
Tương tự, ta có: 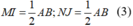
Mà theo giả thiết: AB = CD = a (4)
Từ (1), (2), (3) và (4) suy ra:
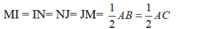
Do đó, tứ giác MJNI là hình thoi ( tính chất hình thoi).
- Gọi O là giao điểm của MN và IJ, ta có:
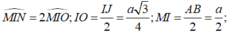
- Xét ΔMIO vuông tại O, ta có:
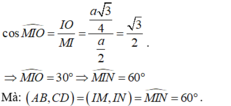

Ta có: A B → . C D → = A B → A D → − A C → = A B → . A D → − A B → . A C →
= A B → . A D → . cos B A D − A B → . A C → cos B A C
= A B 2 . cos 60 ° − A B 2 cos 60 ° (do AB = AC = AD và B A C ^ = B A D ^ = 60 ° )
= 0
Suy ra A B ⊥ C D hay góc giữa hai vecto A B → và C D → là 90 ° .
ĐÁP ÁN C
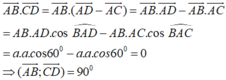



Ủa bạn, đề hỏi góc giữa vectơ AB và IJ cơ mà?