BK
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
1
20 tháng 1 2022
\(\cos A=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{8^2+10^2-13^2}{2\cdot8\cdot10}=-\dfrac{1}{32}< 0\)
nên \(\widehat{A}>90^0\)
=>ΔABC tù
6 tháng 6 2023
a: Số đường chéo là:
\(\dfrac{24\left(24-3\right)}{2}=12\cdot21=252\)
b: 24 đỉnh =>12 đường kính
chọn 1 đường kính =>Sẽ có 22 điểm còn lại
=>Có 22*12=264 tam giác vuông
8 tháng 6 2023
a: Số đường chéo là 24*21/2=21*12=336(đường chéo)
b: Số tam giác vuông tạo thành là:12*22=264 tam giác
9 tháng 6 2023
a. Để tính số đường chéo của một đa giác đều n đỉnh, ta dùng công thức: số đường chéo = n(n-3)/2. Áp dụng vào trường hợp này, ta có số đường chéo của đa giác đều 24 đỉnh là: 24(24-3)/2 = 276 đường chéo.
b. Để lập được một tam giác vuông từ các đỉnh của đa giác đều 24 đỉnh, ta cần chọn 3 đỉnh sao cho 2 trong số đó nằm trên cùng một đường kính của đa giác. Có tổng cộng 24 cách chọn đỉnh trên đường kính và vì mỗi tam giác vuông sẽ được lập bởi 2 đường kính khác nhau, nên số tam giác vuông lập được từ các đỉnh của đa giác đều 24 đỉnh là: 24 x 12 = 288 tam giác vuông. Tuy nhiên, một số tam giác vuông sẽ bị lặp lại khi ta quay đa giác, do đó số tam giác vuông duy nhất là: 288/24 = 12 tam giác vuông.
c. Để lập được một tam giác đều từ các đỉnh của đa giác đều 24 đỉnh, ta cần chọn 3 đỉnh liên tiếp trên đường tròn ngoại tiếp đa giác. Có tổng cộng 24 cách chọn 3 đỉnh liên tiếp, do đó số tam giác đều lập được từ các đỉnh của đa giác đều 24 đỉnh là: 24 tam giác đều.
d. Để lập được một tứ giác từ các đỉnh của đa giác đều 24 đỉnh, ta cần chọn 4 đỉnh bất kỳ. Có tổng cộng C(24,4) cách chọn 4 đỉnh, do đó số tứ giác lập được từ các đỉnh của đa giác đều 24 đỉnh là: C(24,4) = 10626 tứ giác.
e. Để lập được một hình chữ nhật từ các đỉnh của đa giác đều 24 đỉnh, ta cần chọn 4 đỉnh sao cho 2 đỉnh đối diện của hình chữ nhật nằm trên cùng một đường kính của đa giác. Có tổng cộng 24 cách chọn đỉnh trên đường kính và vì mỗi hình chữ nhật sẽ được lập bởi 2 đường kính khác nhau, nên số hình chữ nhật lập được từ các đỉnh của đa giác đều 24 đỉnh là: 24 x 12 = 288 hình chữ nhật. Tuy nhiên, trong số đó có 24 hình vuông, do đó số hình chữ nhật mà không phải là hình vuông là: 288 - 24 = 264 hình chữ nhật.
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
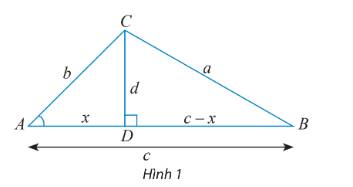
a) ? = x vì \(\cos A = \frac{{AD}}{{AC}} = \frac{x}{b} \Rightarrow ? = x.\)
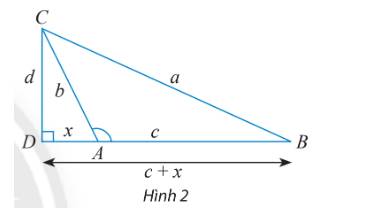
b) Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c + x)^2} = {d^2} + {x^2} + {c^2} + 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = - \cos \widehat {DAC} = - \frac{x}{b} \Rightarrow x = - b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
c) Ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Mà \(\widehat A = {90^o} \Rightarrow \cos A = \cos {90^o} = 0.\)
\( \Rightarrow {a^2} = {b^2} + {c^2}\)
10 tháng 10 2017
a.
Gọi (D):y=ax+b chứa điểm A, C
(D'):y=a'x+b' chứa điểm B, C
* Ta có: A thuộc (D) khi 1= 2a+b (1)
C thuộc (D) khi 4= 3a+b (2)
Giải hệ (1), (2) ta suy ra a=3 , b=-5
* Ta có: B thuộc (D') khi 3=6a'+b' (3)
C thuộc (D') khi 4=3a'+b' (4)
Giải hệ (3), (4) ta suy ra a=-1/3 , b= 5
Ta thấy: a.a' = 3.(-1/3)=-1
Suy ra (D) vuông góc (D') tại điểm chung C của của 2 cạnh (5)
Vậy tam giác ABC vuông tại C
Theo công thức tính cạnh của đoạn thẳng trong hệ trục tọa độ ta có:
AC=\(\sqrt{\left(x_A-x_C\right)^2+\left(y_A-y_C\right)^2}=\sqrt{\left(2-3\right)^2+\left(1-4\right)^2}\)\(=\sqrt{10}\)
BC=\(\sqrt{\left(x_B-x_C\right)^2+\left(y_B-y_C\right)^2}=\sqrt{\left(6-3\right)^2+\left(3-4\right)^2}\)\(=\sqrt{10}\)
Vậy AC=BC (6)
Từ (5) và (6) ta suy ra tam giác ABC vuông cân tại C
SABC=\(\dfrac{1}{2}\).AB.BC=\(\dfrac{1}{2}.\sqrt{10}.\sqrt{10}=\dfrac{1}{2}.10=\)5 (đvdt)
b. Làm tương tự câu a tìm độ dài các cạnh AB, BD, DA và tính diện tích bằng công thức SABD=\(\sqrt{p\left(p-AB\right)\left(p-BD\right)\left(p-DA\right)}\) với p là nửa chu vi tam giác ABD \(p=\dfrac{1}{2}\left(AB+BD+DA\right)\)
Tiếp tục dùng công thức SABD=\(=\dfrac{1}{2}.AB.BD.sinB\) các số liệu nêu trên đã có, chỉ cần thế vào là có góc B
Gọi I là tâm. Tìm độ dài bán kình bằng công thức SABD=\(\dfrac{AB.BD.DA}{4AI}\)
ta tìm được độ dài AI còn cách xác định tâm thì dựa vào giao điểm 2 đường thẳng (d) chứa đoạn AI và (d') chứa đoạn BI là xong
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
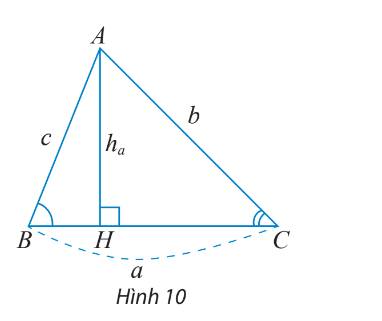
a) Diện tích S của tam giác ABC là: \(S = \frac{1}{2}a.{h_a}\)
b) Xét tam giác vuông AHC ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b}\)
\( \Rightarrow {h_a} = b.\sin C\)
c) Thay \({h_a} = b.\sin C\) vào công thức diện tích, ta được: \(S = \frac{1}{2}ab\sin C\)
d) Theo định lí sin ta có: \(\frac{c}{{\sin C}} = 2R \Rightarrow \sin C = \frac{c}{{2R}}\)
Thay vào công thức ở c) ta được: \(S = \frac{1}{2}ab\frac{c}{{2R}} = \frac{{abc}}{{4R}}.\)
Công thức Heron được áp dụng cho tất cả tam giác nên nó cũng được áp dụng cho tam giác tù hoặc vuông.