Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}-\dfrac{1}{d'}\Leftrightarrow\dfrac{1}{20}=\dfrac{1}{d'}-\dfrac{1}{60}\Leftrightarrow\dfrac{1}{d'}=\dfrac{1}{15}\Rightarrow d'=15\left(cm\right)\)
Chiều cao của ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Leftrightarrow\dfrac{12}{h'}=\dfrac{60}{15}\Leftrightarrow h'=3\left(cm\right)\)

a. Xét tam giác \(OAB\sim\) tam giác \(OA'B'\):
\(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}=\dfrac{OI}{A'B'}\) ( do OI = A'B' ) (1)
Xét tam giác \(OIF'\sim\) tam giác \(A'B'F'\)
\(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}\)
\(\Leftrightarrow\dfrac{OA}{OA'}=\dfrac{OF'}{OA'-OF'}\)
\(\Leftrightarrow\dfrac{30}{OA'}=\dfrac{10}{OA'-10}\)
\(\Leftrightarrow OA'=15\left(cm\right)\)
Thay \(OA'=15\) vào (1) \(\Rightarrow\dfrac{30}{15}=\dfrac{2}{A'B'}\)
\(\Leftrightarrow A'B'=1\left(cm\right)\)
b. Khi vật dịch chuyển rất xa thấu kính thì cho ảnh thật cách thấu kính bằng tiêu cự là 10 cm

Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}-\dfrac{1}{d'}\Rightarrow\dfrac{1}{5}=\dfrac{1}{2}-\dfrac{1}{d'}\Rightarrow d'=\dfrac{10}{3}cm\)
Ảnh cao:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{2}{h'}=\dfrac{2}{\dfrac{10}{3}}\Rightarrow h'=\dfrac{10}{3}cm\)

Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{30}+\dfrac{1}{d'}\Leftrightarrow d'=60cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{2}{h'}=\dfrac{30}{60}\Rightarrow h'=4cm\)

a) Sử dụng hai trong ba tia đặc biệt để vẽ ảnh.
b) Dựa vào tam giác đồng dạng, suy ra h’ = h; d’ = d = 2f.
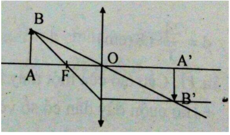

C5:
Đặt vật AB trong khoảng tiêu cự.
+ Ảnh của vật AB tạo bởi thấu kính hội tụ lớn hơn vật (H.45.2).
+ Ảnh của vật AB tạo bởi thấu kính phân kì nhỏ hơn vật (H.45.3)
C7:
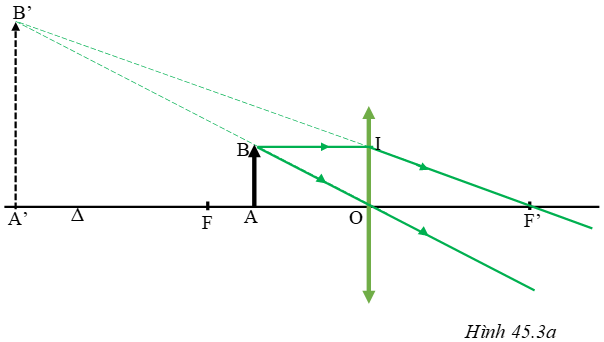
- Xét 2 cặp tam giác đồng dạng trong hình 45.2: OB'F' và BB'I; OAB và OA'B'
Từ hệ thức đồng dạng, ta tính được h' = 3h = l,8cm; OA' = 24cm.
- Xét hai cặp tam giác đồng dạng trong hình 45.3: FB'O và IB'B; OA'B' và OAB.
Từ hệ thức đồng dạng, ta tính được: h' = 0,36cm; OA' = 4,8cm.
+ Ảnh của vật AB tạo bởi thấu kính phân kì nhỏ hơn vật (H.45.3).
C5.
+ Thấu kính là hội tụ: Ảnh của vật AB (hình 45.4) tạo bởi thấu kính hội tụ lớn hơn vật.
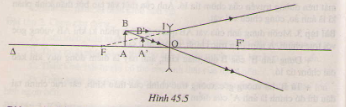
+ Thấu kính là phân kì: Ảnh của vật AB(hình 45.5) tạo bởi thấu kính phân kì nhỏ hơn vật.
C7.
Tam giác BB'I đồng dạng với tam giác OB'F' cho ta:
BIOF=BB′OB′BIOF=BB′OB′ => 812=BB′OB′812=BB′OB′ => 128=OB′BB′128=OB′BB′ => BB′+OBBB′BB′+OBBB′ = 1,5
1 + OBBB′OBBB′ = 1,5 => OBBB′OBBB′ = 0,5 = 1212 => BB′OBBB′OB = 2
Tam giác OAB đồng dạng với tam giác OA'B', cho ta:
OA′OA=A′B′AB=OB′OBOA′OA=A′B′AB=OB′OB (*)
Ta tính tỉ số: OB′OBOB′OB = OB+BB′O
a. Bạn tự vẽ ( ảnh thật )
b.Xét tam giác \(OAB\sim\) tam giác \(OA'B'\)
\(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}=\dfrac{OI}{A'B'}\) ( do OI = AB ) (1)
Xét tam giác \(OIF'\sim\) tam giác \(A'B'F'\)
\(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}=\dfrac{OF'}{OA'-OF'}\)
\(\Leftrightarrow\dfrac{60}{OA'}=\dfrac{20}{OA'-20}\)
\(\Leftrightarrow OA'=30\left(cm\right)\)
Thế \(OA'=30\) vào (1) \(\Leftrightarrow\dfrac{60}{30}=\dfrac{2}{A'B'}\)
\(\Leftrightarrow A'B'=1\left(cm\right)\)