Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) AE//MC,ME//AC=>AEMC là hình bình hành
=>ME=AC
CM tương tự có ADMB là hình bình hành=>AB=MD
gọi P,Q lần lượt là giao của ABvới ME và AC với MD
Có AP//MQ,AQ//MP=>APMQ là hình bình hành=>góc BAC=góc DME
Chứng minh được tam giác ABC=tam giác MDE(c.g.c)
b)AEMC,ADMB là hình bình hành=>AM cắt CE tại trung điểm của mỗi đường,AM cắt BD tại trung điểm của mỗi đường
=>AM,BD,CE đồng quy(đpcm)
Bài 1:
a)Có góc EAC=90 độ+góc BAC=góc FAB
tam giác EAC=tam giác BAF do EA=AB(tam giác AEB vuông cân tại A)
AF=AC(tam giác AFC vuông cân tại A),góc EAB=góc BAF
=>EC=BF(đpcm)
b)Trên tia đối tia MA,lấy điểm N sao cho M là trung điểm của AN
=>AM=AN/2
Có M là trung điểm của BC=>ABNC là hình bình hành
=>NC=AB=AE,BN=AC=AF,góc BAC+góc ACN=180 độ(AB//NC)
Mà góc EAF+góc BAC=180 độ
=>góc EAF=góc ACN
tam giác EAF=tam giác NCA(do EA=NC,AF=CA,góc EAF=góc NCA)
=>góc NAC=góc EFA và AN=EF
Mà AM=AN/2=>AM=EF/2
Gọi H là giao của AM và EF
Có góc NAC+góc HAF=90.Mà góc NAC=góc EFA
=>góc HAF+góc HFA=90 độ=>góc AHF =90 độ
=>AM vuông góc với EF tại H

a) Ta có: \(\widehat{EAC}=\widehat{EAB}+\widehat{BAC}=90^0+\widehat{BAC}\)
\(\widehat{BEF}=\widehat{CAF}+\widehat{BAC}=90^0+\widehat{BAC}\)
suy ra: \(\widehat{EAC}=\widehat{BAF}\)
Xét \(\Delta EAC\)và \(\Delta BAF\)có:
\(EA=BA\) (gt)
\(\widehat{EAC}=\widehat{BAF}\) (cmt)
\(AC=AF\) (gt)
suy ra: \(\Delta EAC=\Delta BAF\) (c.g.c)
\(\Rightarrow\)\(EC=BF\); \(\widehat{ACE}=\widehat{AFB}\) (1)
Gọi O là giao điểm của AC và BF; K là giao điểm của EC và BF
\(\Rightarrow\)\(\widehat{AOF}=\widehat{KOC}\) (2)
\(\Delta AOF\)\(\perp\)\(A\)
\(\Rightarrow\)\(\widehat{AFO}+\widehat{FOA}=90^0\) (3)
Từ (1), (2) và (3) suy ra:
\(\widehat{KOC}+\widehat{OCK}=90^0\)
\(\Rightarrow\)\(\widehat{OKC}=90^0\)
\(\Rightarrow\)\(BF\)\(\perp\)\(CE\)
3.1.Bài tập 1: 62- BTNC&MSCĐ/117)
Tam giác ABC và tam giác A'B'C' có AB=A'B', AC= A'C'. Hai góc A và A'bù nhau. Vẽ trung tuyến AM rồi kéo dài một đoạn MD=MA.
Chứng minh: a. góc ABD = góc A'
b. AM = 1/2 B'C'
( Bạn giải bài trên là có đáp án bài dưới)
Ta thấy: ABC và EAF có hai cặp cạnh bằng nhau và một cặp góc xen giữa chúng bù nhau nên trung tuyến AM = EF

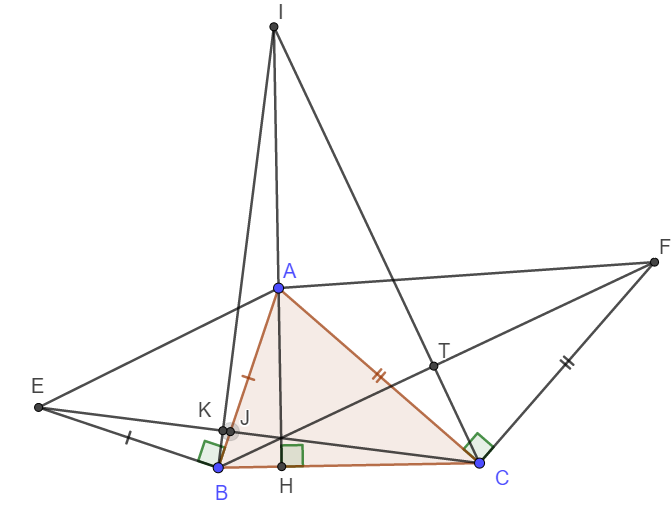
a) Ta có \(\widehat{AHB}=90^o\)
Theo tính chất góc ngoài của tam giác, ta có:
\(\widehat{IAB}=\widehat{AHB}+\widehat{HBA}=90^o+\widehat{HBA}=\widehat{EBA}+\widehat{HBA}=\widehat{CBE}\)
Xét tam giác ABI và tam giác BEC có:
AI = BC (gt)
BA = EB (gt)
\(\widehat{IAB}=\widehat{CBE}\) (cmt)
\(\Rightarrow\Delta ABI=\Delta BEC\left(c-g-c\right)\)
b) Do \(\Delta ABI=\Delta BEC\Rightarrow BI=EC\)
Gọi giao điểm của EC với AB và BI lần lượt là J và K.
Do \(\Delta ABI=\Delta BEC\Rightarrow\widehat{KBJ}=\widehat{BEK}\)
Vậy thì \(\widehat{KBJ}+\widehat{KJB}=\widehat{BEK}+\widehat{KJB}=90^o\)
Suy ra \(\widehat{BKJ}=90^o\) hay \(BI\perp CE\)
c) Chứng minh hoàn toàn tương tự ta có \(IC\perp BF\)
Gọi giao điểm của IC và BF là T.
Xét tam giác IBC có IH, CK, BT là các đường cao nên chúng đồng quy tại một điểm.
Vậy AH, EC, BF đồng quy tại một điểm.
Vẽ hình đi bạn
Rồi mình giúp bạn làm
Vẽ hình xong gửi tin nhắn cho mình
:) Chúc bạn học tôt
@@

a) Ta có \(\widehat{AHB}=90^o\)
Theo tính chất góc ngoài của tam giác, ta có:
\(\widehat{IAB}=\widehat{AHB}+\widehat{HBA}=90^o+\widehat{HBA}=\widehat{EBA}+\widehat{HBA}=\widehat{CBE}\)
Xét tam giác ABI và tam giác BEC có:
AI = BC (gt)
BA = EB (gt)
\(\widehat{IAB}=\widehat{CBE}\) (cmt)
\(\Rightarrow\Delta ABI=\Delta BEC\left(c-g-c\right)\)
b) Do \(\Delta ABI=\Delta BEC\Rightarrow BI=EC\)
Gọi giao điểm của EC với AB và BI lần lượt là J và K.
Do \(\Delta ABI=\Delta BEC\Rightarrow\widehat{KBJ}=\widehat{BEK}\)
Vậy thì \(\widehat{KBJ}+\widehat{KJB}=\widehat{BEK}+\widehat{KJB}=90^o\)
Suy ra \(\widehat{BKJ}=90^o\) hay \(BI\perp CE\)
c) Chứng minh hoàn toàn tương tự ta có \(IC\perp BF\)
Gọi giao điểm của IC và BF là T.
Xét tam giác IBC có IH, CK, BT là các đường cao nên chúng đồng quy tại một điểm.
Vậy AH, EC, BF đồng quy tại một điểm.

a) AE//MC,ME//AC=>AEMC là hình bình hành
=>ME=AC
CM tương tự có ADMB là hình bình hành=>AB=MD
gọi P,Q lần lượt là giao của ABvới ME và AC với MD
Có AP//MQ,AQ//MP=>APMQ là hình bình hành=>góc BAC=góc DME
Chứng minh được tam giác ABC=tam giác MDE(c.g.c)
b)AEMC,ADMB là hình bình hành=>AM cắt CE tại trung điểm của mỗi đường,AM cắt BD tại trung điểm của mỗi đường
=>AM,BD,CE đồng quy(đpcm)
Bài 1:
a)Có góc EAC=90 độ+góc BAC=góc FAB
tam giác EAC=tam giác BAF do EA=AB(tam giác AEB vuông cân tại A)
AF=AC(tam giác AFC vuông cân tại A),góc EAB=góc BAF
=>EC=BF(đpcm)
b)Trên tia đối tia MA,lấy điểm N sao cho M là trung điểm của AN
=>AM=AN/2
Có M là trung điểm của BC=>ABNC là hình bình hành
=>NC=AB=AE,BN=AC=AF,góc BAC+góc ACN=180 độ(AB//NC)
Mà góc EAF+góc BAC=180 độ
=>góc EAF=góc ACN
tam giác EAF=tam giác NCA(do EA=NC,AF=CA,góc EAF=góc NCA)
=>góc NAC=góc EFA và AN=EF
Mà AM=AN/2=>AM=EF/2
Gọi H là giao của AM và EF
Có góc NAC+góc HAF=90.Mà góc NAC=góc EFA
=>góc HAF+góc HFA=90 độ=>góc AHF =90 độ
=>AM vuông góc với EF tại H

thay câu b vào câu c , ta có : 2b +5 + 7b là số nguyên tố
=> 9b + 5 là số nguyên tố (*)
thay (*) vào câu a , ta có :
9b + 6 chia hết cho b
=> 3( 3b +2 ) chia hết cho b
mà ( 3 ; b ) =1
=>3b + 2 chia hết cho b
lại có :
b chia hết cho b
=>3b chia hết cho b
=>3b + 2 - 3b chia hết cho b
=>2 chia hết cho b
=> b = 2 hoặc 1
- nếu b = 1 => thay vào (*) , ta có :
9.1 + 5 là số nguyên tố ( loại )
- nếu b = 2 => thay vào (*) , ta có :
9.2 + 5 là số nguyên tố => a = 2.2 + 5 = 9 ( thỏa mãn )
Vậy a = 9 , b = n thì thỏa mãn đề bài . ^^

A B C D E O I M N M P I
Gọi O là giao điểm DC và BE, I là giao điểm DC và AB
Ta có
góc DAB= góc EAC (=90)
góc BAC= góc BAC( góc chung)
-> góc DAB+ góc BAC= góc EAC+ góc BAC
-> góc DAC= góc BAE
Xét tam giác DAC và tam giác BAE ta có
AD=AB ( tam giác ABD vuông cân tại A)
AC=AE ( tam giác AEC vuông cân tại A)
góc DAC=góc BAE ( cmt)
-. tam giac DAC= tam giac BAE (c-g-c)
-> góc DAI= góc IBO ( 2 góc tương ứng)
ta có
góc DAI+ góc DIA=90 ( tam giác DAI vuông tại A)
góc DAI= góc IBO (cmt)
góc DIA= góc BIO ( 2 góc đối đỉnh)
--> góc BIO+góc IBO =90
Xét tam giác BIO ta có
góc BIO + góc IBO + góc BIO=180 ( tổng 3 góc trong tam giác)
90+ goc BIO=180
góc BIO=180-90=90
=> BE vuông góc DC tại O
Xét tam giác DBC ta có
M là trung điểm BD (gt)
P là trung điểm BC (gt)
-> MP la đường trung bình tam giác DBC
-> MP// DC và MP=1/2 DC
cmtt PN là đường trung bình tam giác BEC
-> PN//BE và PN=1/2BE
ta có
DC vuông góc BE tại O (cmt)
DC//MP (cmt)
-> MP vuông góc BE
mà BE// PN (cmt)
nên MP vuông góc PN tại P
--> tam giác MNP vuông tại P (1)
ta có
MP=1/2 DC (cmt)
PN=1/2BE (cmt)
DC=BE ( tam giac DAC = tam giac BAE)
--> MP=PN (2)
từ (1) và (2) suy ra tam giac MNP vuông cân tại P