Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

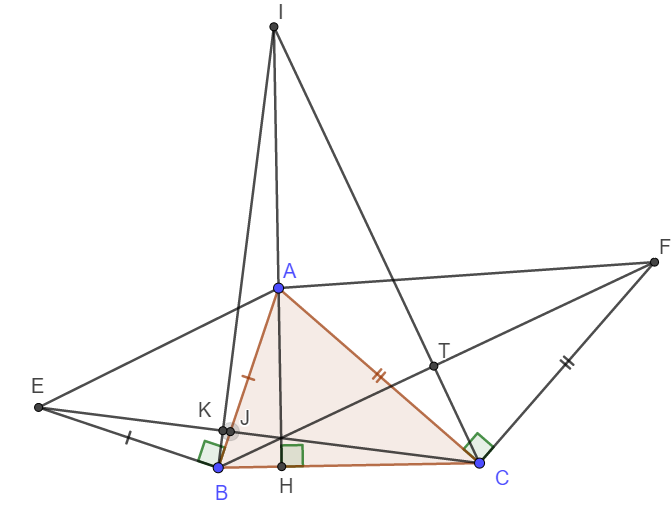
a) Ta có \(\widehat{AHB}=90^o\)
Theo tính chất góc ngoài của tam giác, ta có:
\(\widehat{IAB}=\widehat{AHB}+\widehat{HBA}=90^o+\widehat{HBA}=\widehat{EBA}+\widehat{HBA}=\widehat{CBE}\)
Xét tam giác ABI và tam giác BEC có:
AI = BC (gt)
BA = EB (gt)
\(\widehat{IAB}=\widehat{CBE}\) (cmt)
\(\Rightarrow\Delta ABI=\Delta BEC\left(c-g-c\right)\)
b) Do \(\Delta ABI=\Delta BEC\Rightarrow BI=EC\)
Gọi giao điểm của EC với AB và BI lần lượt là J và K.
Do \(\Delta ABI=\Delta BEC\Rightarrow\widehat{KBJ}=\widehat{BEK}\)
Vậy thì \(\widehat{KBJ}+\widehat{KJB}=\widehat{BEK}+\widehat{KJB}=90^o\)
Suy ra \(\widehat{BKJ}=90^o\) hay \(BI\perp CE\)
c) Chứng minh hoàn toàn tương tự ta có \(IC\perp BF\)
Gọi giao điểm của IC và BF là T.
Xét tam giác IBC có IH, CK, BT là các đường cao nên chúng đồng quy tại một điểm.
Vậy AH, EC, BF đồng quy tại một điểm.
Vẽ hình đi bạn
Rồi mình giúp bạn làm
Vẽ hình xong gửi tin nhắn cho mình
:) Chúc bạn học tôt
@@

a) Ta có \(\widehat{AHB}=90^o\)
Theo tính chất góc ngoài của tam giác, ta có:
\(\widehat{IAB}=\widehat{AHB}+\widehat{HBA}=90^o+\widehat{HBA}=\widehat{EBA}+\widehat{HBA}=\widehat{CBE}\)
Xét tam giác ABI và tam giác BEC có:
AI = BC (gt)
BA = EB (gt)
\(\widehat{IAB}=\widehat{CBE}\) (cmt)
\(\Rightarrow\Delta ABI=\Delta BEC\left(c-g-c\right)\)
b) Do \(\Delta ABI=\Delta BEC\Rightarrow BI=EC\)
Gọi giao điểm của EC với AB và BI lần lượt là J và K.
Do \(\Delta ABI=\Delta BEC\Rightarrow\widehat{KBJ}=\widehat{BEK}\)
Vậy thì \(\widehat{KBJ}+\widehat{KJB}=\widehat{BEK}+\widehat{KJB}=90^o\)
Suy ra \(\widehat{BKJ}=90^o\) hay \(BI\perp CE\)
c) Chứng minh hoàn toàn tương tự ta có \(IC\perp BF\)
Gọi giao điểm của IC và BF là T.
Xét tam giác IBC có IH, CK, BT là các đường cao nên chúng đồng quy tại một điểm.
Vậy AH, EC, BF đồng quy tại một điểm.

Em tham khảo tại đây nhé.
Câu hỏi của Đức Tạ - Toán lớp 7 - Học toán với OnlineMath

a) Tam giác ABI và BEC có: AI = BC, \(\widehat{BAI}=\widehat{EBC}\left(=90^o+\widehat{ABH}\right)\), AB = BE
\(\Rightarrow\Delta ABI=\Delta BEC\left(c.g.c\right)\)
b) Từ câu a => BI = CE và \(\widehat{ABI}=\widehat{BEC}\Rightarrow\widehat{ABI}+\widehat{EBI}=\widehat{BEC}+\widehat{EBI}=90^o\Rightarrow BI⊥CE\)
c) Chứng minh tương tự ta được \(CI⊥BF\)
Xét tam giác BIC có AH, CE, BF là ba đường cao nên đồng quy tại một điểm.
Em tham khảo tại đây nhé.
Câu hỏi của Đức Tạ - Toán lớp 7 - Học toán với OnlineMath

Em tham khảo tại đây nhé.
Câu hỏi của Đức Tạ - Toán lớp 7 - Học toán với OnlineMath
AH ở đâu v bn ?
a) Ta có góc AHB = 90
Theo tính chất góc ngoài của tam giác, ta có:
góc IAB= góc AHB + gócHBA = 90 + góc HBA = góc EBA + góc HBA = CBE
Xét tam giác ABI và tam giác BEC có:
AI = BC (gt)
BA = EB (gt)
góc IAB = CBE (cmt)
⇒ΔABI = ΔBEC c − g − c
b) Do ΔABI = ΔBEC⇒BI = EC
Gọi giao điểm của EC với AB và BI lần lượt là J và K.
Do ΔABI = ΔBEC⇒ = Vậy thì góc KBJ + góc KJB = góc BEK + góc KJB = 90
Suy ra góc BKJ = 90 hay BI⊥CE
c) Chứng minh hoàn toàn tương tự ta có IC⊥BF
Gọi giao điểm của IC và BF là T.
Xét tam giác IBC có IH, CK, BT là các đường cao nên chúng đồng quy tại một điểm.
Vậy AH, EC, BF đồng quy tại một điểm