Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=5cm\)
Theo định lí Pytago tam giác MNP vuông tại N
\(NP=\sqrt{MP^2-MN^2}=6cm\)
b, Xét tam giác ABC và tam giác NPM có
^BAC = ^PNM = 900
\(\dfrac{AB}{NP}=\dfrac{AC}{NM}=\dfrac{3}{6}=\dfrac{4}{8}=\dfrac{1}{2}\)
Vậy tam giác ABC ~ tam giác NPM ( c.g.c )

a: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
\(NP=\sqrt{10^2-8^2}=6\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔNPM vuông tại N có
AB/NP=AC/NM
Do đó: ΔABC\(\sim\)ΔNPM

Bài giải:
SADEF=\(\dfrac{\left(AD+EF\right).FG}{2}=\dfrac{\left(4+2\right).2}{2}=6\left(cm^2\right)\)
SABCD=\(\dfrac{\left(AD+BC\right).BG}{2}=\dfrac{\left(4+1\right).1}{2}=2,5\left(cm^2\right)\)
=> SABCDEF= SADEF+SABCD= 6+2,5=8,5(cm2)
b) SDEA=\(\dfrac{DE.AE}{2}=\dfrac{4.3}{2}=6\left(cm^2\right)\)
SDCFE=\(\dfrac{\left(DE+CF\right).EF}{2}=\dfrac{\left(4+8\right).4}{2}=24\left(cm^2\right)\)
SCFB=\(\dfrac{CF.FB}{2}=\dfrac{8.6}{2}=24\left(cm^2\right)\)
=> SABCD=SDEA+SDCFE+SCFB=6+24+24=54(cm2)

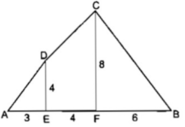
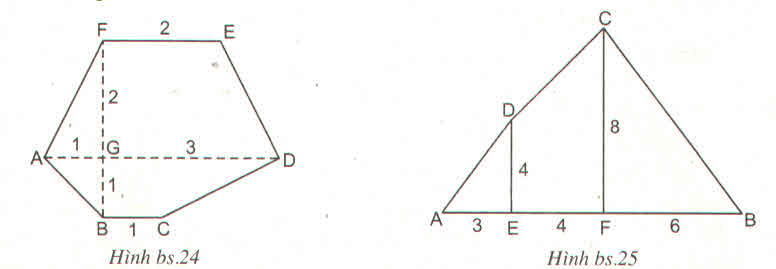
Chia đa giác ABCD thành tam giác vuông AED, hình thang vuông EDCF và tam giác vuông FCB.
S A E D = 1/2 AE.DE = 1/2. 3. 4 = 6( c m 2 )
S E D C F = (ED + FC)/2. EF = (4 + 8)/2. 4 = 24 ( c m 2 )
S C F B = 1/2 CF. FB = 1/2 .8 .6 = 24 ( c m 2 )
S A B C D = S A E D + S E D C F + S C F B = 6 + 24 + 24 = 54 ( c m 2 )


hì hì xin hình:>
Hình đâu ạ