Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

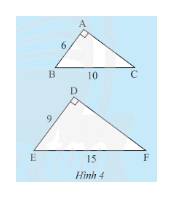
a) Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {6^2} + A{C^2} = {10^2} \Leftrightarrow A{C^2} = {10^2} - {6^2} = 64 \Leftrightarrow AC = 8\).
Xét tam giác \(DEF\) vuông tại \(D\) ta có:
\(D{E^2} + D{F^2} = E{F^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {9^2} + D{F^2} = {15^2} \Leftrightarrow D{F^2} = {15^2} - {9^2} = 144 \Leftrightarrow DF = 12\).
b) Tỉ số:
\(\frac{{AB}}{{DE}} = \frac{6}{9} = \frac{2}{3};\frac{{AC}}{{DF}} = \frac{8}{{12}} = \frac{2}{3}\); \(\frac{{BC}}{{EF}} = \frac{{10}}{{15}} = \frac{2}{3}\).
Do đó, \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\).
c) Xét tam giác\(ABC\) và tam giác\(DEF\) có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta DEF\) (c.c.c)

a,Xét tam giác ADE va tam giác ACB :
Có:AE/AB=3/9=1/3
 góc chung
AD/AC=4/12=1/3
=>tg ADE đồng dạng tg ACB(cgc)
=>AD/AC=AE/AB
b, Vì tg ADE đồng dạng tg ACB(cmt)
=> AD/AC=AE/AB=DE/CB
Mà:AD/AC=AE/AB=1/3
=>DE/CB=1/3

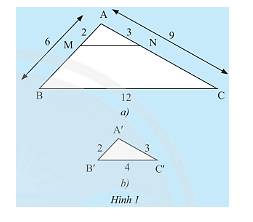
a) Ta có: \(\frac{{A'B'}}{{AB}} = \frac{2}{6} = \frac{1}{3},\frac{{A'C'}}{{AC}} = \frac{3}{9} = \frac{1}{3},\frac{{B'C'}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\). Do đó, các tỉ số trên bằng nhau.
b) Ta có: \(\frac{{AM}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{3}{9} = \frac{1}{3}\)
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC\) (định lí Thales đảo)
Vì \(MN//BC \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (Hệ quả của định lí Thales)
Do đó, \(\frac{{MN}}{{BC}} = \frac{1}{3} \Leftrightarrow \frac{{MN}}{{12}} = \frac{1}{3} \Rightarrow MN = \frac{{12.1}}{3} = 4\).
Vậy \(MN = 4cm\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
Xét tam giác \(AMN\) và tam giác \(A'B'C'\) ta có:
\(AM = A'B' = 2cm;AN = A'C' = 2cm;MN = B'C' = 4cm\)
Do đó, \(\Delta AMN = \Delta A'B'C'\) (c.c.c)
Vì \(\Delta AMN = \Delta A'B'C'\) nên \(\Delta AMN\backsim\Delta A'B'C'\) (2)
Từ (1) và (2) suy ra, \(\Delta ABC\backsim\Delta A'B'C'\).

bài1
a) EF=??
b) không đồng dạng
c) không đồng dạng
d) Đồng dạng (vì sao thì bạn nhắn cho mình nha)
các cặp góc bằng nhau ABC=DEF; BCA=EFD; CAB=FDE
bài 2
a) theo tính chất đường trung bình trong mỗi tam giác (không hiểu thì nhắn cho mình)
ta có MN=1/2AB => MN/AB=1/2 (1)
NM=1/2BC => NP/BC=1/2 (2)
MP=1/2AC => MP/AC=1/2 (3)
từ (1),(2),(3) => MNP đồng dạng với ABC
b) vì MNP đồng dạng với ABC với tỉ số k là 2 ( theo câu a)
nên chu vi ABC = 2 lần chu vi MNP =40cm

a) Ta có: \(\dfrac{AN}{AB}=\dfrac{3}{6}=\dfrac{1}{2}\)
\(\dfrac{AM}{AC}=\dfrac{4.5}{9}=\dfrac{1}{2}\)
Do đó: \(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)\(\left(=\dfrac{1}{2}\right)\)
Xét ΔANM và ΔABC có
\(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)(cmt)
\(\widehat{BAC}\) chung
Do đó: ΔANM\(\sim\)ΔABC(c-g-c)

Ta có: \(\frac{{AB}}{{DE}} = 2{;^{}}\frac{{BC}}{{EF}} = 2{;^{}}\frac{{AC}}{{DF}} = 2\)
Ta có:\(\dfrac{AB}{DE}=2;\dfrac{BC}{EF}=2;\dfrac{AC}{DF}=2\)
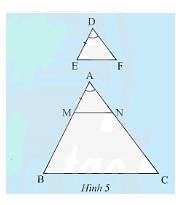
a) Vì \(MN//BC\left( {M \in AB,N \in AC} \right)\) nên \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\)(định lí Thales).
b) Vì \(AM = DE\) mà \(\frac{{DE}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AM}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{3} \Rightarrow AN = \frac{1}{3}AC\).
Lại có \(DF = \frac{1}{3}AC\) nên \(AN = DF = \frac{1}{3}AC\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
d) Dự đoán hai tam giác \(DEF\) và \(ABC\) đồng dạng.