Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAEF có
H,M lần lượt là trung điểm của AE,AF
nên HM là đường trung bình
=>HM//EF
=>EF vuông góc với AE
Ta có: ΔAEF vuông tại E
mà EM là đường trung tuyến
nên EM=MF
b: Xét tứ giác ABFC có
M là trung điểm chung của FA và BC
nên ABFC là hình bình hành
Suy ra: AB=FC
Xét ΔBAE có
BH là đường cao, là đường trung tuyến
nên ΔBAE cân tại B
=>BA=BE=CF
c: Vì ABFC là hình bình hành
nên AC//BF
d: Vì EF//HM
nên EF//BC

a: Xét ΔAEF có
H,M lần lượt là trung điểm của AE,AF
nên HM là đường trung bình
=>HM//EF
=>EF vuông góc với AE
Ta có: ΔAEF vuông tại E
mà EM là đường trung tuyến
nên EM=MF
b: Xét tứ giác ABFC có
M là trung điểm chung của FA và BC
nên ABFC là hình bình hành
Suy ra: AB=FC
Xét ΔBAE có
BH là đường cao, là đường trung tuyến
nên ΔBAE cân tại B
=>BA=BE=CF
c: Vì ABFC là hình bình hành
nên AC//BF
d: Vì EF//HM
nên EF//BC

A B C D E H M
a/ Xét 2 tam giác EMC và tam giác AMB có:
BM=MC (gt)
AM=ME (gt)
Góc AMB=góc EMC (2 góc đối đỉnh)
=> tam giác EMC = tam giác AMB (Cạnh-góc-cạnh)
=> AB=EC (2 cạnh tương ứng)
b/ Xét tam giác ADE có:
AH=HD (gt)
AM=ME (gt)
=> HM là đường trung bình của tam giác ADE => HM//DE => AD vuông góc DE (1)
và DE/2=HM (Tính chất đường trung bình)
Mà DF=FE=DE/2
=> DF=HM=DE/2 (2)
Từ (1) và (2) => Tứ giác HMFD là hình chữ nhật => MF vuông góc DE
c/ MF//DH (cmt)
=> MF//AD

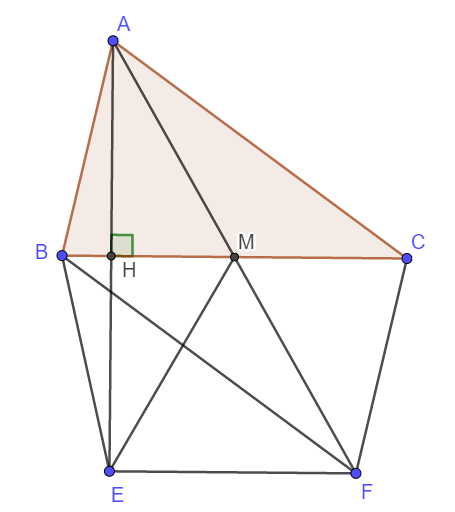
a) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên nó là tam giác cân.
Vậy thì MA = ME. Lại có MA = MF nên ME = MF.
b) Do AME là tam giác cân, MH là đường cao nên MH cũng là phân giác.
Vậy thì \(\widehat{AMB}=\widehat{BME}\)
Mà \(\widehat{AMB}=\widehat{CMF}\Rightarrow\widehat{BME}=\widehat{CMF}\)
Xét tam giác BME và CMF có:
BM = CM
ME = MF
\(\widehat{BME}=\widehat{CMF}\)
\(\Rightarrow\Delta BME=\Delta CMF\left(c-g-c\right)\)
\(\Rightarrow BE=CF\)
c) Dễ thấy \(\Delta BMF=\Delta CMA\left(c-g-c\right)\Rightarrow\widehat{BFM}=\widehat{CAM}\)
Chúng lại ở vị trí so le trong nên AC//BF.
d) Xét tam giác AEF có MA = ME = MF nên AEF là tam giác vuông. Vậy \(AE\perp EF\)
Lại có \(AE\perp BC\Rightarrow\) BC//EF