

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét ΔAHE vuông tại H và ΔADB vuông tại D có
góc DAB chung
Do đó: ΔAHE đồng dạng với ΔADB
Suy ra: AH/AD=AE/AB
hay \(AH\cdot AB=AE\cdot AD\)
c: \(AE\cdot AD-HA\cdot HB\)
\(=AH\cdot AB-AH\cdot HB=AH\cdot AH=AH^2\)

a: Xét ΔCDE vuông tại D và ΔCAB vuông tại A có
góc ACB chung
Do dó ΔCDE đồng dạng với ΔCAB
=>CD/CA=CE/CB
=>CD/CE=CA/CB
=>ΔCDA đồng dạng với ΔCEB
=>EB/DA=BC/AC
mà BC/AC=AC/CH
nên EB/DA=AC/CH=BA/HA
=>BE/AD=BA/HA
=>\(BE=\dfrac{AB}{AH}\cdot AD=\dfrac{AB}{AH}\cdot\sqrt{AH^2+HD^2}\)
\(=\dfrac{AB}{AH}\cdot\sqrt{AH^2+AH^2}=AB\sqrt{2}\)
b: Xét ΔABE vuông tại A có sin AEB=AB/BE=1/căn 2
nên góc AEB=45 độ
=>ΔABE vuông cân tại A
=>AM vuông góc với BE
BM*BE=BA^2
BH*BC=BA^2
Do đó: BM*BE=BH/BC
=>BM/BC=BH/BE
=>ΔBMH đồng dạng với ΔBCE

Từ hình vẽ thì hướng giải như sau:
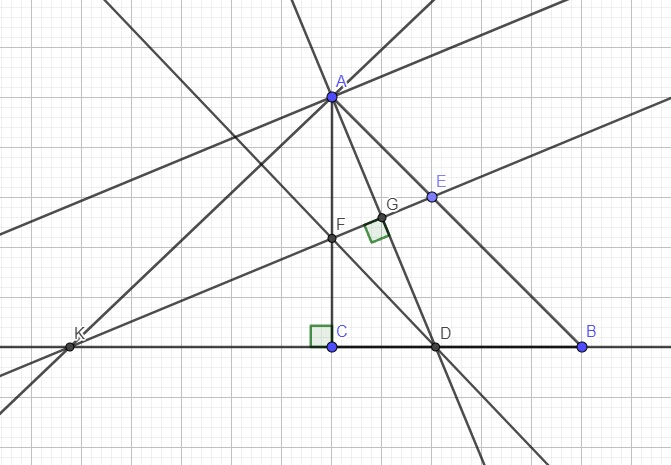
Dễ dàng nhận ra \(DF\perp AK\), từ đó biết vtpt của DF \(\Rightarrow\) phương trình DF
\(\Rightarrow\) Tọa độ F (là giao của DF và đường tròn tâm D bán kính DE do DE=DF)
Biết tọa độ F \(\Rightarrow\) viết được pt AD qua D vuông góc EF
\(\Rightarrow\) Tọa độ A từ là giao AK và AD
\(\Rightarrow\) Phương trình AB qua A và E, phương trình AC qua A và F, phương trình BC qua D và vuông góc AF

a)Xét tam giác ACD và tam giác ECD(đều là vuông)![]()
ECD=DCA(Vì CD là p/giác)
CD là cạnh chung
\(\Rightarrow\)tam giác ACD=tam giác ECD(cạnh huyền góc nhọn)
b)Vì tam giác ACD=tam giác ECD(cạnh huyền góc nhọn)
\(\Rightarrow\)AD=DE(cạnh cặp tương ứng)
\(\Rightarrow\)D cách đều hai mút của AE
\(\Rightarrow\)CD là đường trung trực của AE
Do đó CI\(\perp\)AE
\(\Rightarrow\)Tam giác CIE là tam giác vuông
c)Vì AD=DE(câu b)
Mà tam giác BDE là tam giác vuông(tại E)
\(\Rightarrow\)DE<BD(cạnh góc vuông nhỏ hơn cạnh huyền)
\(\Rightarrow\)AD<BD(đpcm)
d)Kéo dài BK cắt AC tại O
Vì BK\(\perp\)CD(gt)
\(\Rightarrow\)CK là đường cao thứ nhất của tam giác OBC(1)
Vì tam giác ABC vuông tại A
Nên BA\(\perp\)AC
\(\Rightarrow\)BA là đường cao thứ hai của tam giác OBC(2)
Theo đề bài ta có DE\(\perp\)BC
Nên DE là đường cao thứ ba của tam giác OBC(3)
Từ (1),(2) và (3) suy ra:
Ba đường cao giao nhau tại một điểm trùng với điểm D
\(\Rightarrow\) 3 đường thẳng AC;DE;BK đồng quy(đpcm)

a: \(AH=\sqrt{BH\cdot CH}=6\left(cm\right)\)
\(AB=\sqrt{BC^2-AC^2}=\sqrt{13^2-\left(3\sqrt{13}\right)^2}=2\sqrt{13}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{\sqrt{13}}\)
nên \(\widehat{B}=56^0\)
b: Xét ΔAHB vuông tại H và ΔCEH vuông tại E có
\(\widehat{BAH}=\widehat{C}\)
Do đó: ΔAHB\(\sim\)ΔCEH
Suy ra: \(\dfrac{AH}{CE}=\dfrac{BH}{EH}\)
hay \(AH\cdot HE=CE\cdot BH\)