Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
b: BH=CH=BC/2=6/2=3(cm)
nên AH=4(cm)
c: G là trọng tâm của ΔABC
nên CG cắt AB tại trung điểm của BA
=>F là trung điểm của AB
G là trọng tâm của ΔBAC
nên AG=2GH
=>GD=2GH
hay H là trung điểm của GD
Xét tứ giác BGCD có
H là trung điểm của GD
H là trung điểm của BC
Do đó: BGCD là hình bình hành
Suy ra: BD=GC
=>BD=2/3CF

a) tam giác cân nên dg cao cx là dg trung tuyến
=>BH=3
áp dụng pitago vs tam giác AHB tìm ra dc AH=4
b) vì AH cx là trung tuyến =>G thuộc AH =>A,G,H thẳng hàng
c) xét tam giác ABG và tam giác ACG có
BAH=HAC( dg cao cx là dg trung tuyến
AG chung
AB=AC
=>...

a: Xét ΔCDE vuông tại D và ΔCAB vuông tại A có
góc ACB chung
Do dó ΔCDE đồng dạng với ΔCAB
=>CD/CA=CE/CB
=>CD/CE=CA/CB
=>ΔCDA đồng dạng với ΔCEB
=>EB/DA=BC/AC
mà BC/AC=AC/CH
nên EB/DA=AC/CH=BA/HA
=>BE/AD=BA/HA
=>\(BE=\dfrac{AB}{AH}\cdot AD=\dfrac{AB}{AH}\cdot\sqrt{AH^2+HD^2}\)
\(=\dfrac{AB}{AH}\cdot\sqrt{AH^2+AH^2}=AB\sqrt{2}\)
b: Xét ΔABE vuông tại A có sin AEB=AB/BE=1/căn 2
nên góc AEB=45 độ
=>ΔABE vuông cân tại A
=>AM vuông góc với BE
BM*BE=BA^2
BH*BC=BA^2
Do đó: BM*BE=BH/BC
=>BM/BC=BH/BE
=>ΔBMH đồng dạng với ΔBCE

a: Xét (O) có
góc BEC, góc BDC đều là các góc nội tiếp chắn nửa đường tròn
=>góc BEC=góc BDC=90 độ
=>CE vuông góc AB, BD vuông góc AC
Xét ΔABC có
CE,BD là đường cao
CE cắt BD tại H
=>H là trực tâm
=>AH vuông góc BC tại F
góc BEH+góc BFH=180 độ
=>BEHF nội tiếp
b: Xét ΔHCB có CO/CB=CM/CH
nên OM//BH
=>góc COM=góc CBH
=>góc COM=góc FEC
=>góc MOF+góc FEM=180 độ
=>OMEF nội tiếp

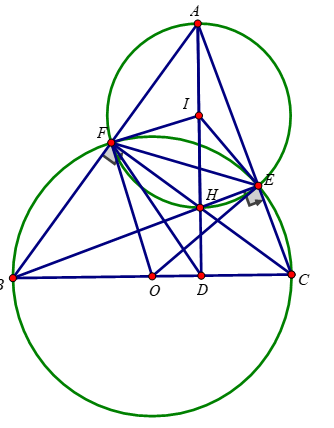
\(\text{a) Ta có:}\)
∠BFC = 90o (góc nội tiếp chắn nửa đường tròn)=> ∠AFC = 90o
∠BEC = 90o (góc nội tiếp chắn nửa đường tròn)=> ∠AEC = 90o
Tứ giác AEHF có:
∠AFC = 90o
∠AEC = 90o
=>∠AFC + ∠AEC = 180o
=> AEHF là tứ giác nội tiếp
b) ∠AFH = 90o => AH là đường kính đường tròn ngoại tiếp tứ giác AEHF
\(\text{Do đó trung điểm I của AH là tâm đường tròn ngoại tiếp tứ giác AEHF}\)
=> Bán kính đường tròn ngoại tiếp tứ giác AEHF là R = AI = \(\frac{AH}{2}\) = 2cm
Ta có: ∠BAC = 60o
=> ∠FIE = 2∠BAC = 120o (Góc nội tiếp bằng \(\frac{1}{2}\) góc ở tâm cùng chắn một cung)
=> Số đo ∠EHF = 120o
Diện tích hình quạt IEHF là:
\(S=\frac{\pi R^2N}{360}=\frac{\pi.2^2.120}{360}=\frac{4\pi}{3}\left(ĐVDT\right)\)
\(\text{c) Xét tam giác ABC có: }\)
BE và CF là các đường cao
BE giao với CF tại H
=> H là trực tâm tam giác ABC
=>AH ⊥ BC hay ∠ADC = ∠ADB = 90o
Xét tứ giác BEFC có:
∠BFC = ∠BEC = 90o
=> 2 đỉnh E, F cùng nhìn cạnh BC dưới 1 góc bằng nhau
=> BEFC là tứ giác nội tiếp
=> ∠HFE = ∠BEC ( 2 góc nội tiếp cùng chắn cung EC) (1)
Xét tứ giác BFHD có:
∠BFH = ∠HDB = 90o
=>∠BFH + ∠HDB = 180o
=> Tứ giác BFHD là tứ giác nội tiếp ( tổng 2 góc đối bằng 180o)
=> ∠DFH = ∠BEC ( 2 góc nội tiếp cùng chắn cung HD) (2)
Từ (1) và (2) = > ∠HFE = ∠DFH
=> FH tia phân giác của góc ∠DFE
d) Tam giác OFB cân tại O => ∠OFB = ∠FBO
Tam giác BFC vuông tại F => ∠FBO + ∠HCD = 90o
=> ∠OFB + ∠HCD = 90o (*)
\(\hept{\begin{cases}\Delta FIH\text{CÂN TẠI I}\\\widehat{IHF}=\widehat{DHC}\left(\text{ĐỐI ĐỈNH}\right)\\\Delta HDC\text{VUÔNG TẠI D}\Rightarrow\widehat{DHC}+\widehat{HDC}=90^0\end{cases}}\Rightarrow\widehat{IFH}+\widehat{HDC}=90^0\)
Từ (*) và (**) => ∠OFB = ∠IFH
=> ∠OFB + ∠OFH = ∠IFH + ∠OFH <=> ∠BFC = ∠FIO <=> ∠FIO) = 90o
Vậy FI là tiếp tuyến của (O)
Chứng minh tương tự EI là tiếp tuyến của (O)
Mà I là trung điểm của AH
=> Tiếp tuyến của (O) tại E và F và AH đồng quy tại 1 điểm.
HÌNH THÌ VÀO THỐNG KÊ HỎI ĐÁP CỦA MIK NHA
VCN JACK trả lời cuc64 kì đ luôn . đ là chất
Toán hình học lớp 7 học kì 2