Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

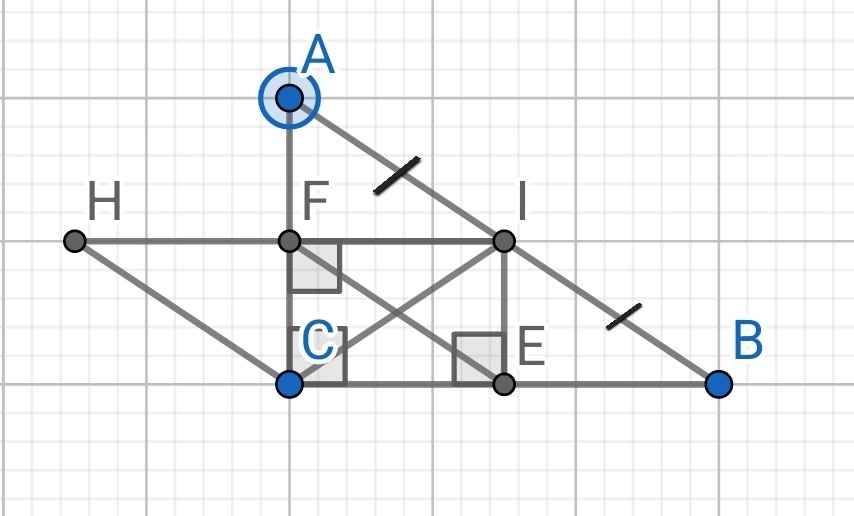 *) Tứ giác CEIF là hình gì?
*) Tứ giác CEIF là hình gì?
Tứ giác CEIF có:
∠CEI = ∠CFI = ∠ECF = 90⁰ (gt)
⇒ CEIF là hình chữ nhật
*) Do CEIF là hình chữ nhật (cmt)
⇒ FI = CE và FI // CE
Do FI // CE (cmt)
⇒ FH // CE
Do FI = CE (cmt)
FI = FH (gt)
⇒ FH = CE
Tứ giác CHFE có:
FH // CE (cmt)
FH = CE (cmt)
⇒ CHFE là hình bình hành
Sửa đề: IF vuông góc AC tại F
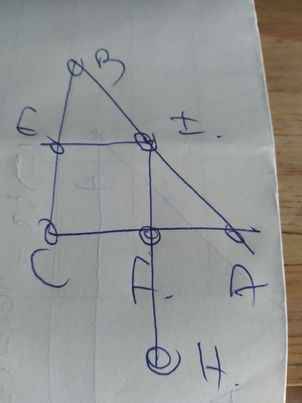
a: Xét tứ giác CEIF có
\(\widehat{CEI}=\widehat{CFI}=\widehat{FCE}=90^0\)
Do đó: CEIF là hình chữ nhật
b: CEIF là hình chữ nhật
=>CE//FI và CE=FI
CE=FI
FI=FH
Do đó: CE=FH
CE//FI
\(F\in IH\)
Do đó: CE=FH
Xét tứ giác CEFH có
CE//FH
CE=FH
Do đó: CEFH là hình bình hành

a: Xét tứ giác AEIF có
\(\widehat{AEI}=\widehat{AFI}=\widehat{FAE}=90^0\)
Do đó: AEIF là hình chữ nhật

a: Xét tứ giác AMIN có
\(\widehat{AIM}=\widehat{AIN}=\widehat{NAM}=90^0\)
Do đó: AMIN là hình chữ nhật

a)Ta có
BK=KC (GT)
AK=KD( Đối xứng)
suy ra tứ giác ABDC là hình bình hành (1)
mà góc A = 90 độ (2)
từ 1 và 2 suy ra tứ giác ABDC là hình chữ nhật
b) ta có
BI=IA
EI=IK
suy ra tứ giác AKBE là hình bình hành (1)
ta lại có
BC=AD ( tứ giác ABDC là hình chữ nhật)
mà BK=KC
AK=KD
suy ra BK=AK (2)
Từ 1 và 2 suy ra tứ giác AKBE là hình thoi
c) ta có
BI=IA
BK=KC
suy ra IK là đường trung bình
suy ra IK//AC
IK=1/2AC
mà IK=1/2EK
Suy ra EK//AC
EK=AC
Suy ra tứ giác AKBE là hình bình hành
B A C D E K

a: Xét tứ giác ANMP có
\(\widehat{ANM}=\widehat{APM}=\widehat{PAN}=90^0\)
Do đó: ANMP là hình chữ nhật

a: Xét tứ giác CEIF có
\(\widehat{CEI}=\widehat{CFI}=\widehat{FCE}=90^0\)
Do đó: CEIF là hình chữ nhật
giải giúp mình với