Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔCHA vuông tại H và ΔCHM vuông tại H có
CH chung
HA=HM
=>ΔCHA=ΔCHM
=>góc ACH=góc MCH
=>CH là phân giác của góc ACM
b: Xét ΔAHC vuông tại H và ΔMHD vuông tại H có
HA=HM
góc HAC=góc HDM
=>ΔHAC=ΔHMD
=>HC=HD
=>AM là trung trực của CD

a) Xét tam giác AHB và tam giác AHE có
BH=HE
AH chung
góc AHE= góc AHB= 90 độ ( AH vuông góc với BC)
=> tam giác AHB= tam giác AHE (c.g.c)
=>HE=HB
b) Xét tam giác AHB và tam giác DHE có
góc DHE = góc AHB ( đối đỉnh)
HE=HB (cmt)
AH=HD
=> tam giác AHB=tam giác DHE (c.g.c)
=> DE= AB ( 2 cạnh tương ứng)
=> tam giác DHE= tam giác AHE =tam giác AHB
=> AE=DE(2 cạnh tương ứng)
c) Xét tam giác AHC và tam giác DHC có
HC chung
góc AHE=góc DHE=90 độ
AH=HD
=> tam giác AHC= tam giác DHC( cạnh huyền-góc nhọn)
=>AC=DC (2 cạnh tương ứng)
Xét tam giác ACE và tam giác DCE có
AE= DE (cmt)
AC= DC(cmt)
CE chung
=> tam giác ACE= tam giác DCE(c.c.c)
=> góc EAC= góc EDC (2 góc tương ứng)
d)Ta có: C,E,B thẳng hàng
=> góc CEA+ góc AEB= 180 độ
Mà góc CEN và góc AEB là 2 góc đối đỉnh
=>góc AEC+ góc CEN= 180 độ
=> A,E,N thẳng hàng

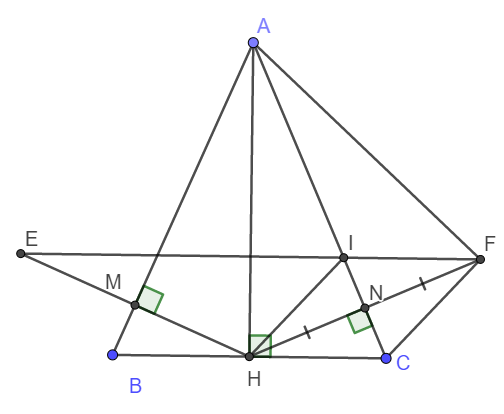
a) Do ABC là tam giác cân tại A nên AH là đường cao hay đồng thời là đường phân giác.
Xét tam giác vuông AMH và tam giác vuông ANH có:
Cạnh AH chung
\(\widehat{MAH}=\widehat{NAH}\)
\(\Rightarrow\Delta AMH=\Delta ANH\) (Cạnh huyền - góc nhọn)
\(\Rightarrow HM=HN.\)
b) Dễ dàng thấy ngay AC là đường trung trực của HF.
Khi đó thì AH = AF; CH = CF
Xét tam giác AHC và tam giác AFC có:
Cạnh AC chung
AH - AF
CH = CF
\(\Rightarrow\Delta AHC=\Delta AFC\left(c-c-c\right)\)
\(\Rightarrow\widehat{AFC}=\widehat{AHC}=90^o\Rightarrow AF\perp CF.\)
c) Ta thấy ngay \(\Delta HIN=\Delta FCN\left(g-c-g\right)\)
\(\Rightarrow IN=CN\)
Xét tam giác vuông INF và tam giác vuông CNH có:
HN = FN
IN = CN
\(\Rightarrow\Delta INF=\Delta CNH\) (Hai cạnh góc vuông)
\(\Rightarrow\widehat{IFN}=\widehat{CHN}\)
Mà chúng lại ở vị trí so le trong nên IF // BC.
d) Chứng minh tương tự câu c, ta có IE // BC
Vậy thì qua I có hai tia IE và IF cùng song song với BC nên chúng trùng nhau.
Vậy I, E, F thẳng hàng.

chotamgiacabc
gggfffffffffffffffffffffffffwuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuueahhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhgggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggg

a)Xet 2 tam giac vuong AHB va DHC co:
HC chung
DH = AH
=>\(\Delta\)AHB = \(\Delta\)AHC (2 canh goc vuong)
Ta co : CA=CD (2 canh tuong ung)
=>\(\Delta\)CAD can
b)