Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


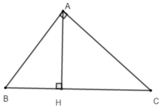
Trong tam giác AHB có AH + BH > AB (bất đẳng thức trong tam giác)
Trong tam giác AHC có AH + HC > AC (bất đẳng thức trong tam giác)
Khi đó cộng vế theo vế ta được: AH + BH + AH + HC > AB + AC
Hay 2AH + (BH + HC) > AB + AC
Hay 2AH + BC > AB + AC
Vậy 2AH + BC > AB + AC.
Chọn đáp án A

a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: BH=CH
b: BH=CH=6cm
=>AH=8cm
c: Xét ΔAHE có
AK là đường cao
AK là đường trung tuyến
Do đó: ΔAHE cân tại A
hay AE=AH
d: Xét ΔADH có
AI là đường cao
AI là đườngtrung tuyến
Do đó:ΔADH cân tại A
=>AD=AH=AE
=>ΔADE cân tại A

A B C H
Vì tam giác ABC vuông tại A
nên AB2+AC2=BC2=92=81(Định lí Py-ta-go)
Ta có: AB:AC=3:4 => AB/3=AC/4 =>AB2/9=AC2/16
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
AB2/9=AC2/16\(=\frac{AB^2+AC^2}{9+16}=\frac{81}{25}\)
Do đó, *)AB2=81/25*9=29,16
=>AB=5,4(AB E N)(cm)
*)AC2=81/25*16=51,84
=>AC=7,2(AC E N)(cm)
SABC=\(\frac{BC\cdot AH}{2}=\frac{9\cdot AH}{2}\)(Diện tích hình tam giác)(1)
SABC=\(\frac{AB\cdot AC}{2}=\frac{7,2\cdot5,4}{2}=\frac{38,88}{2}\)(Diện tích hình tam giác)(2)
Từ (1);(2) =>9*AH=38,88
AH=38,88/9
AH=4,32(cm)
Vậy AH=4,32 cm


a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>góc BAH=góc CAH
=>AH là phân giác của góc BAC
b: BH=CH=12/2=6cm
AH=căn 10^2-6^2=8cm

a: Ta có: ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=10^2-6^2=64\)
=>\(AH=\sqrt{64}=8\left(cm\right)\)
b: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
c: Ta có: ΔAHB=ΔAHC
=>BH=CH
Xét ΔBMH vuông tại M và ΔCNH vuông tại N có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔBMH=ΔCNH
d: Xét ΔABO vuông tại B và ΔACO vuông tại C có
AO chung
AB=AC
Do đó: ΔABO=ΔACO
=>OB=OC
=>ΔOBC cân tại O

Đặt\(\frac{AB}{3}=\frac{AC}{4}=k\) suy ra: AB=3k ; AC=4k
Tam giác ABC vuông tại A nên:
\(BC^2=AB^2+AC^2\) ( định lý Pytago)
\(9^2=\left(3k\right)^2+\left(4k\right)^2\)
\(81=9.k^2+16.k^2\)
\(81=25k^2\)
\(\Rightarrow k^2=\frac{81}{25}\)
\(\Rightarrow k=\frac{9}{5}\) ( do k>0)
\(\Rightarrow AB=\frac{27}{5};AC=\frac{36}{5}\)
Tam giác ABC vuông tại A nên
AB.AC=AH.BC
\(\frac{27}{5}.\frac{36}{5}=9.AH\)
\(\Rightarrow\)AH = \(\frac{972}{25}:9\)=4,32