Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)
MB=MC
Do đó: ΔMAB=ΔMEC

tu ve hinh nha
XÉT TAM GIÁC MAB VÀ TAM GIÁC MEC CO:
BM=CM( M LÀ TRUNG ĐIỂM CỦA BC)
GÓC BMA = GÓC CME( 2 GÓC ĐỐI ĐỈNH)
AM=EM(GT)
=>TAM GIÁC MAB = TAM GIÁC MEC( C-G-C)

a: Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMEC
b: Sửa đề: AB//EC
Ta có: ΔMAB=ΔMEC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CE
c: Ta có: AB//CE
AB\(\perp\)AC
Do đó: CE\(\perp\)CA
Xét ΔECA vuông tại C và ΔBAC vuông tại A có
EC=BA
AC chung
Do đó: ΔECA=ΔBAC
=>EA=BC
Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)
MC=MB
Do đó ΔMAC=ΔMEB
=>AC=BE
Xét ΔBEC và ΔCAB có
BE=CA
EC=AB
BC chung
Do đó: ΔBEC=ΔCAB
=>\(\widehat{BEC}=\widehat{CAB}=90^0\)
=>ΔBEC vuông tại E
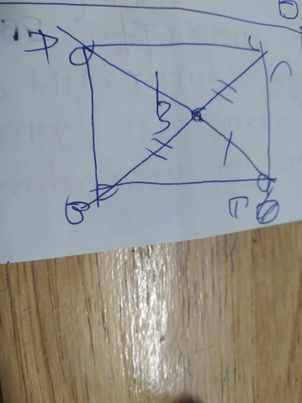

a) Xét \(\Delta MAB\)và \(\Delta MEC\)có:
MB = MC (M là trung điểm của BC)
\(\widehat{AMB}=\widehat{CME}\)(2 góc đối đỉnh)
MA = ME (gt)
\(\Rightarrow\Delta MAB=\Delta MEC\left(c-g-c\right)\)
b) Ta có: \(\Delta MAB=\Delta MEC\)(theo a)
\(\Rightarrow\widehat{MAB}=\widehat{MEC}\)(2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow EC//AB\)
\(\Rightarrow\widehat{ECA}+\widehat{CAB}=180^o\)(2 góc trong cùng phía)
\(\Rightarrow\widehat{ECA}+90^o=180^o\)
\(\Rightarrow\widehat{ECA}=90^o\Rightarrow EC\perp AC\)
c) Ta có: \(\Delta MAB=\Delta MEC\)(theo a)
\(\Rightarrow AB=EC\)(2 cạnh tương ứng)
Xét \(\Delta CME\)và \(\Delta AMB\)có:
ME = MA (gt)
\(\widehat{CME}=\widehat{AMB}\)(2 góc đối đỉnh)
EC = AB (cmt)
=> \(\Delta CME=\Delta AMB\left(c-g-c\right)\)
\(\Rightarrow CM=AM\)(2 cạnh tương ứng)
Mà BC = 2.CM
=> BC = 2.AM (đpcm)