Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ADME là hình chữ nhật vì có 3 góc vuông: \(\widehat{A}\)= \(\widehat{D}\)= \(\widehat{E}\)= 900
b) Để ADME là hình vuông thì AM là phân giác \(\widehat{A}\)
Vậy M là giao đường phân giác góc A với BC thì ADME là hình vuông

a)xét tứ giác ADME có
\(\widehat{A}\) = 90°(do ΔABC vuông tại A)
\(\widehat{ADM} = 90°\)(do MD⊥AB)
\(\widehat{AEM} = 90°\)(do ME ⊥ AC)
nên ADEM là hình chữ nhật
b) Ta có:
ME = MK = \(\dfrac{EK}{2}\)( do M là trung điểm EK) (1)
DA = AI = \(\dfrac{DI}{2}\)( do A là trung điểm DI) (2)
Mà AD = ME (do ADME là hcn) (3)
Từ (1),(2),(3)
⇒ EK = DI
Mặt khác EK // DI (do AD // ME)
Nên DKEI là hbh
⇒ DK // EI và DK = EI

Em tham khảo bài toán tương tự tại link dưới đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath

a: Xét tứ giác AIMJ có
\(\widehat{AIM}=\widehat{AJM}=\widehat{JAI}=90^0\)
=>AIMJ là hình chữ nhật
b: AIMJ là hình chữ nhật
=>MI//AJ và MI=AJ
MI=AJ
MN=MI
Do đó: MN=AJ
MI//AJ
N\(\in\)MI
Do đó: MN//JA
Xét tứ giác AMNJ có
AJ//MN
AJ=MN
Do đó: AMNJ là hình bình hành

a: Xét tứ giac AEMD có
góc AEM=góc ADM=góc DAE=90 độ
nen AEMD là hình chữ nhật
b: Xét ΔAMP có
AB vừa là đường cao, vừa là trung tuyến
nên ΔAMP cân tại A
=>AB là phân giác của góc MAP(1)
Xét ΔAMK có
AC vừa là đường cao, vừa là trung tuyến
nên ΔMKA cân tại A
=>AC là phân giác của góc MAK(2)
Từ (1), (2) suy ra góc KAP=2*90=180 độ
=>K,A,P thẳng hàng
mà AK=AP
nên A là trung điểm của KP
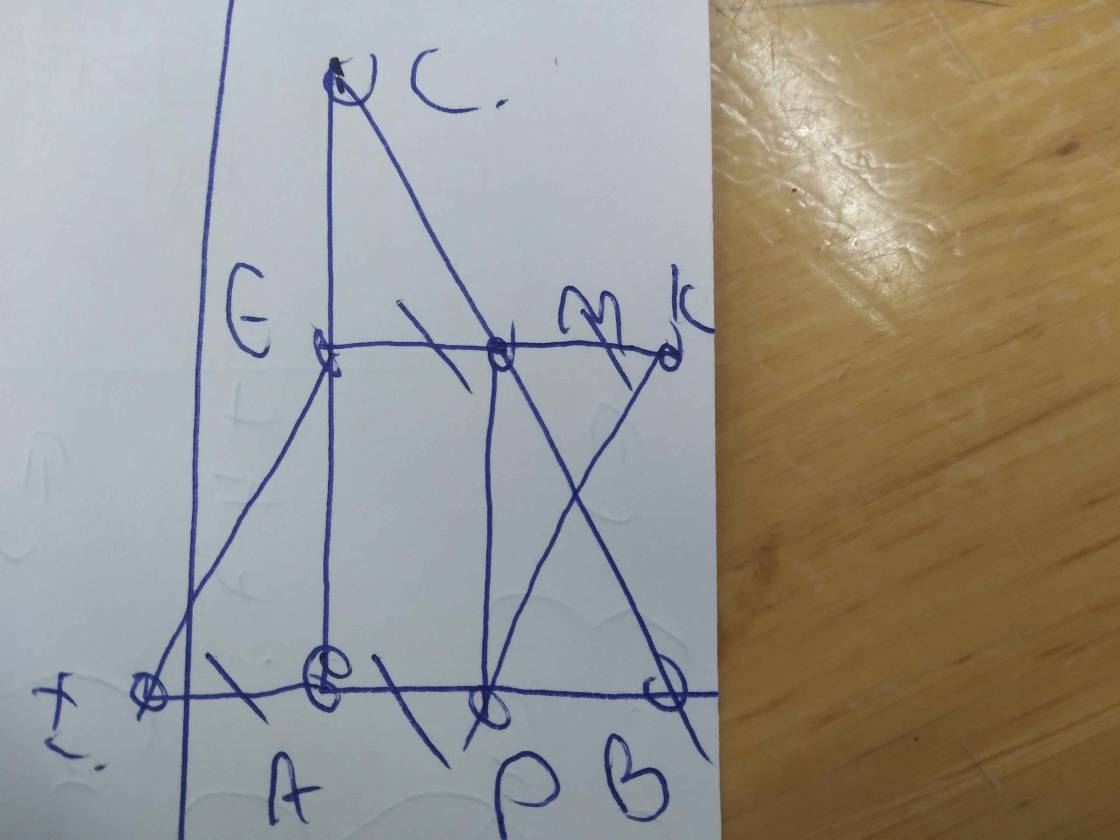


a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
b: ADME là hình chữ nhật
=>AD//EM và AD=EM(1)
M là trung điểm của EK
=>\(EK=2EM\left(2\right)\)
A là trung điểm của ID
=>\(ID=2DA\left(3\right)\)
Từ (1),(2),(3) suy ra EK=ID
EM//AD
K\(\in\)EM
I\(\in\)AD
Do đó: EK//ID
Xét tứ giác EKDI có
EK//DI
EK=DI
Do đó: EKDI là hình bình hành
Căng quá ! Bro có bộ não to đấy