Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, chứng minh tứ giác ADHB nội tiếp, xác định tâm O đường tròn ngoại tiếp tứ giác.
Ta có:
ADB^ = 1v (gt)
AHB^ = 1v (gt)
=> ABHD nội tiếp đường tròn đường kính AB.
Tâm O là trung điểm AB.
b, chứng minh góc EAD bằng HBD và OD song song HB:
Ta có:
EAD^ = ABD^ (1) ( có cạnh L)
BD là phân giác nên:
ABD^ = HBD^ (2)
(1) và (2) => EAD^ = HBD^.
*cm OD song song HB:
tam giác BOD cân và có góc AOD là góc ngoài của tam giác BOD => AOD^ = 2.ABD^ = ABC^
=> OD //Bc vì có 2 góc ở vị trí đồng vị = nhau.
c, chứng minh tứ giác HCED nội tiếp:
Ta có:
CHD^ = 90*- AHD^
mà AHD^ = ABE^ ( cùng chắn cung AD)
=> CHD^ = 90* - ABE^ (1)
mặt khác:
BEC^ = 180* - AEB^
mà AEB^ = 90 - ABE^
=> BEC^ =180* - 90* + ABE^ = 90* + ABE^ (2)
(1) + (2):
CHD^ + BEC^ = 90* - ABE^ + 90* + ABE^ = 180*
vậy tứ giác HCED nội tiếp đường tròn.
d, cho biết góc ABC bằng 60 độ và AB = a (a> 0 cho trước). Tính theo a diện tích tam giác ABC phần nằm ngoài đường tròn O:
Diện tích tam giác ABC phần nằm ngoài đường tròn (gọi là S) là phần diện tích giới hạn bỡi AC, AH và cung (ADH). và S = diện tích tam giác ABC - diện tích giới hạn bỡi AB, BH và cung (ADH) (gọi là S1)
* tính S(ABC):
tam giác L ABH có:
AH = a.sin 60* = a.√3/2
BH = a/2 ( đối diện góc 30* = 1/2 cạnh huyền)
tam giác L ABC có:
BC = a/cos 60* = 2a.
=> S(ABC) = AH.BC/2 = (a.√3/2).(2a)/2 = a^2√3/2
* tính S1:
dễ thấy:S(BOH) = S(ABH)/2 = AH.BH/4 = (a.√3/2).(a/2)/4 = a^2√3/16
tam giác cân OBH có OBH^ = 60* => BOH^ = 60*
S3 = diện tích hình quạt OBH = (60*/360*).OB^2.TT = 1/6.a^2/4.TT = a^2.TT/24
S4 =diện tích giới hạn bỡi BH và cung (BH) = S3 - S(BOH)
= a^2.TT/24 - a^2√3/16 = a^2(TT/3 -√3/2)/8
S1 = diện tích 1/2 đường tròn - S4
= a^2.TT/8 - a^2(TT/3 -√3/2)/8
= a^2(TT - TT/3 + √3/2)/8
= a^2(2TT/3 + √3/2)/8
vậy:
S = S(ABC) - S1 = a^2√3/2 - a^2(2TT/3 + √3/2)/8
=(a^2/2).[(√3 - (2TT/3 + √3/2)/4]
= a^2(45√3 -4TT)/96
-----bạn kiểm tra lại số liệu tính toán.
Bài 2:
a, Chứng minh AM. AE = AC^2:
(AB) là kí hiệu cung AB
Ta có:
sđ ACM^ = sđ (AM)/2 = sđ(AC -CM)/2 = sđ AEB^
=> tam giác ACM đồng dạng với ACE. (g.g.g) cho ta:
AC/AE =AM/AC =>AM. AE = AC^2
b, DM cắt BC tại I, AI cắt đường tròn O tại N. Chứng minh D, N, E thẳng hàng.
tam giác ADE có
DM L AE ( AMD^ = 1v góc nội tiếp chăn1/2 đường tròn)
EH L AD ( H là giao của AD và BE)
vậy EH và DM là 2 đường cao
=> AI L DE
mặt khác
DN L AI ( góc AND^ nội tiếp chắn 1/2 đường tròn)
=> DN // DE và có D chung => D, N, E thẳng hàng.
c, Cho BAC = 45độ. Tính theo R chu vi hình phẳng giới hạn bởi AB, AC và cung BDC:
Ta có:
BOC^ = 2.BAC^ = 90*
( góc ở tâm = 2 lần góc nội tiếp cùng chắn cung BC.
=> cung (BDC) = 2.TT.R/4 = TT.R/2
tam giác BOC là tam giác L cân tại O nên:
BC = R.√2 => BH = BC/2=R.√2/2
tam giác BHO là tam giác L cân, cho ta:
BH = OH = R.√2/2.
=> AH = OH + OA = R.√2/2 +R = R(1+√2/2)
tam giác L AHB có:
AB^2 = AH^2 + BH^2
= R^2.(1+√2/2)^2 + R^2/2
= R^2(1 + √2 + 1/2 + 1/2)
= R^2.(2+√2)
=> AB = R√(2 +√2 )
mà AB = AC => AB = AC= R√(2 +√2 )
chu vi hình phẳng:
CV=cung (BDC) + AB +AC = TT.R/2 + 2.R√(2 +√2 )
~~~~~~~~~~ai đi qua nhớ để lại ~~~~~~~~~~~~

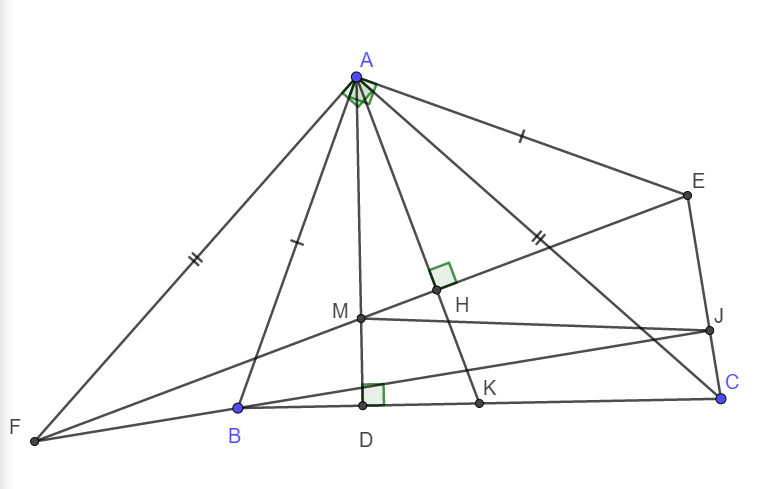
a) Xét tam giác ACK và tam giác FAM có :
AC = FA
\(\widehat{CAK}=\widehat{AFM}\) (Cùng phụ với góc \(\widehat{FAK}\) )
\(\widehat{ACK}=\widehat{FAM}\) (Cùng phụ với góc \(\widehat{DAC}\) )
\(\Rightarrow\Delta ACK=\Delta FAM\left(g-c-g\right)\)
b) Do \(\Delta ACK=\Delta FAM\left(cma\right)\Rightarrow FM=AK\)
Chứng minh hoàn toàn tương tự câu a ta có: \(\Delta ABK=\Delta EAM\left(g-c-g\right)\)
\(\Rightarrow ME=AK\)
Từ đó suy ra FM = ME hay M là trung điểm EF.
c) Kéo dài FB cắt EC tại J. Ta chứng minh \(\widehat{FJE}=90^o\)
Xét tam giác FAB và tam giác CAE có:
FA = CA
AB = AE
\(\widehat{FAB}=\widehat{CAE}\) (Cùng phụ với góc \(\widehat{BAC}\) )
\(\Rightarrow\Delta FAB=\Delta CAE\left(c-g-c\right)\)
\(\Rightarrow FB=CE\) và \(\widehat{AFB}=\widehat{ACE}\)
Xét tứ giác AFJE có:
\(\widehat{AFJ}+\widehat{FJE}+\widehat{JEA}+\widehat{EAF}=360^o\)
\(\Rightarrow\widehat{ACE}+\widehat{FJE}+\widehat{CEA}+\widehat{EAC}+90^o=360^o\)
\(\Rightarrow\widehat{FJE}+\widehat{ACE}+\widehat{CEA}+\widehat{EAC}=270^o\)
\(\Rightarrow\widehat{FJE}+180^o=270^o\)
\(\Rightarrow\widehat{FJE}=90^o\)
Vậy nên \(FB\perp EC\) (đpcm).
Bài 2:
A B C H I M N B' C' D E
a) Gọi giao điểm của đường phân giác ^ABC và ^ACB với AC và AB lần lượt là E và D
Dễ thấy: ^BAH=^ACB (Cùng phụ với ^HAC) => 1/2. ^BAH = 1/2. ^ACB
=> ^DAM=^ACD. Mà ^DAM+^MAC=^BAC=900 => ^ACD+^MAC=900 => AM \(\perp\)CD
hay NI\(\perp\)AM.
Tương tự ta chứng minh MI\(\perp\)AN
Xét tam giác MAN: NI\(\perp\)AM; MI\(\perp\)AN => I là trực tâm của tam giác MAN (đpcm).
b) Do I là trực tâm của tam giác AMN (cmt) => AI\(\perp\)MN hay AI\(\perp\)B'C'
Ta có: Tam giác ABC có 2 đường phân giác ^ABC và ^ACB cắt nhau tại I => AI là phân giác ^BAC
=> AI là phân giác ^B'AC'.
Xét tam giác AB'C': AI là phân giác ^B'AC'. Mà AI\(\perp\)B'C' => Tam giác AB'C' cân tại A
Lại có: ^B'AC'=900 => Tam giác B'AC' vuông cân tại A.

Bài 1:
B D A H C E
Vì CD và CE lần lượt là phân giác trong và phân giác ngoài của góc C nên \(CD\perp CE\)
Kẻ \(CH\perp AB\)thì \(\widehat{CED}=\widehat{HCD}\)cùng phụ với \(\widehat{EDC}\)
Ta có : \(\widehat{HCA}=90^0-\widehat{HAC}=90^0-\left[180^0-\widehat{BAC}\right]=\widehat{BAC}-90^0\)
\(\widehat{ACD}=\frac{1}{2}\widehat{ACB}=\frac{1}{2}\left[180^0-\widehat{ABC}-\widehat{BAC}\right]=90^0-\frac{1}{2}\left[\widehat{ABC}+\widehat{BAC}\right]\)
Do đó \(\widehat{HCD}=\widehat{HCA}+\widehat{ACD}=\frac{\widehat{BAC}-\widehat{ABC}}{2}\)nếu \(\widehat{BAC}>\widehat{ABC}\).
Nếu \(\widehat{BAC}< \widehat{ABC}\)thì \(\widehat{HCD}=\frac{\widehat{ABC}-\widehat{BAC}}{2}\)
Vậy \(\widehat{HCD}=\left|\frac{\widehat{BAC}-\widehat{ABC}}{2}\right|\).
2. Giả sử \(\widehat{B}>\widehat{C}\), ta có : \(\widehat{DAH}=\frac{\widehat{B}-\widehat{C}}{2}\)
Suy ra \(\widehat{B}-\widehat{C}=2\widehat{DAH}=2\cdot15^0=30^0\)
Mặt khác \(\widehat{B}+\widehat{C}=90^0\)từ đó suy ra \(\widehat{B}=60^0,\widehat{C}=30^0\)
Nếu \(\widehat{B}< \widehat{C}\)thì chứng minh tương tự,ta có \(\widehat{B}=30^0,\widehat{C}=60^0\)
P/S : Hình bài 1 chỉ mang tính chất minh họa nhé
Theo yêu cầu vẽ hình của bạn Hyouka :)
2.
: B A C H D TH: ^B > ^C B A C H D TH: ^B < ^C