Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABC và tam giác HAC có :
\(\widehat{BAC}=\widehat{AHC}\left(=90^o\right)\)
Chung \(\widehat{ACB}\)
\(\Rightarrow\) tam giác ABC đồng dạng với tam giác HAC (g-g) (đpcm)
b) Xét tam giác ABC và tam giác HBA có :
\(\widehat{BAC}=\widehat{AHB}\left(=90^o\right)\)
Chung \(\widehat{ABC}\)
\(\Rightarrow\) tam giác ABC đồng dạng với tam giác HBA (g-g)
Mà tam giác ABC đồng dạng với tam giác HAC ( câu a )
Suy ra tam giác HBA đồng dạng với tam giác HAC
\(\Rightarrow\frac{HB}{HA}=\frac{HA}{HC}\Leftrightarrow HA^2=HB\times HC\left(đpcm\right)\)
c) Do \(AH^2=BH\times HC\)
\(\Leftrightarrow AH^2=9\times16\)
\(\Leftrightarrow AH^2=144\)
\(\Leftrightarrow AH=\sqrt{144}\)
\(\Leftrightarrow AH=12\left(cm\right)\)
Áp dụng định lí Py-ta-go cho tam giác AHC vuông tại H ta được :
\(AH^2+HC^2=AC^2\)
\(\Leftrightarrow12^2+16^2=AC^2\)
\(\Leftrightarrow AC^2=400\)
\(\Leftrightarrow AC=\sqrt{400}\)
\(\Leftrightarrow AC=20\left(cm\right)\)
Ta có : \(BC=BH+HC=9+16=25\left(cm\right)\)
Do BE là phân giác của \(\widehat{ABC}\)
\(\Rightarrow\frac{AE}{AB}=\frac{EC}{BC}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được :
\(\frac{AE}{AB}=\frac{EC}{BC}=\frac{AE+EC}{9+25}=\frac{AC}{34}=\frac{20}{34}=\frac{10}{17}\)
\(\Rightarrow\frac{EC}{BC}=\frac{10}{17}\Leftrightarrow\frac{EC}{25}=\frac{10}{17}\Leftrightarrow EC=\frac{250}{17}\left(cm\right)\)
Lại có : \(AE=AC-EC=20-\frac{250}{17}=\frac{90}{17}\left(cm\right)\)
Vậy độ dài đoạn thẳng EC là \(\frac{250}{17}\) cm ; AE là \(\frac{90}{17}\) cm

a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
Do đó: ΔABC\(\sim\)ΔHAC
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
Do đó: ΔHBA\(\sim\)ΔHAC
Suy ra: HB/HA=HA/HC
hay \(HA^2=HB\cdot HC\)

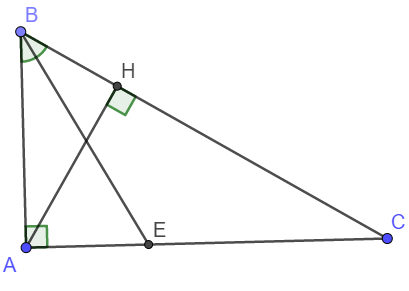
a) Xét tam giác ABC và tam giác HBA có:
\(\widehat{BAC}=\widehat{BHA}=90^o\)
Góc B chung
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right)\)
b)
Xét tam giác ABC và tam giác HAC có:
\(\widehat{BAC}=\widehat{AHC}=90^o\)
Góc C chung
\(\Rightarrow\Delta ABC\sim\Delta HAC\left(g-g\right)\)
c) Từ câu a và b ta có : \(\Delta HBA\sim\Delta HAC\)
\(\Rightarrow\frac{HB}{HA}=\frac{HA}{HC}\Rightarrow HA^2=HB.HC=9.16=144\)
\(\Rightarrow HA=12\left(cm\right)\)
Khi đó áp dụng định lý Pi-ta-go ta có:
\(AB^2=BH^2+AH^2=9^2+12^2\Rightarrow AB=15\left(cm\right)\)
\(AC^2=CH^2+AH^2=16^2+12^2\Rightarrow AC=20\left(cm\right)\)
BC = BH + HC = 9 + 16 = 25 (cm)
Áp dụng tính chất tia phân giác trong tam giác ta có:
\(\frac{AE}{EC}=\frac{AB}{BC}=\frac{15}{25}=\frac{3}{5}\)
\(\Rightarrow AE=\frac{3}{8}\times20=7,5\left(cm\right)\)
\(\Rightarrow EC=20-7,5=12,5\left(cm\right)\)

Tự vẽ hình chỉ bt làm ý a,c, thôi thông cảm T^T
a,Xét ΔHAB và ΔABC
\(\widehat{BHA}=\widehat{BAH}=90^o\)
Góc B chung
\(\Rightarrow\Delta HBA\text{∼ }\Delta ABC\)
c,Xét ΔABC ta có:
BC2=AC2+AB2
BC2=162+122
BC2=400
BC=√400=20cm
Ta có ΔHAB~ΔABC(câu a)
\(\Rightarrow\frac{AH}{AC}=\frac{AB}{BC}\Leftrightarrow\frac{AH}{16}=\frac{12}{20}\)
\(\Rightarrow AH=\frac{12.16}{20}=9,6cm\)
a.Xét \(\Delta HBA\)và \(\Delta ABC\)có
\(\widehat{BHA}=\widehat{BAC}=90^0\)
\(\widehat{B}\) chung
Do đó \(\Delta HBA\)đồng dạng \(\Delta ABC\)\((\)g.g\()\)
b.Từ \(\Delta HBA\)đồng dạng \(\Delta ABC\)
\(\Rightarrow\frac{AH}{AC}=\frac{AB}{BC}\)
\(\Rightarrow AH.BC=AB.AC\)
c.Xét \(\Delta ABC\),có \(\widehat{A}\)=90 độ , theo định lý py -ta -go,ta có
\(BC^2=AB^2+AC^2\)
\(BC^2=12^2+16^2\)
\(BC^2=400\)\(\Rightarrow BC=\sqrt{400}\)
\(BC=20cm\)
Ta có \(\frac{AH}{AC}=\frac{AB}{BC}\Leftrightarrow\frac{AH}{16}=\frac{12}{20}\)
\(\Rightarrow AH=\frac{12\times16}{20}\)
\(\Rightarrow AH=9,6cm\)
Chúc bạn học tốt.Phần d mình chưa giải đc nha

Vì DE la dg pg cua goc ADB (gt)
=.>AD/DB= AE/EB (h chat dg pg trong tam giac) (1)
Vi DF la dg pg cua goc ADC (gt)
=>FC/FA=ĐC/ĐÁ ( tính chất đg pg trong tam giác) (2)
tu (1) va (2) suy ra:EA/EB.FC/FA.DB.DC=AD/DB.DB/DC.DC/DA=1 (dpcm)
Vì DE la dg pg cua goc ADB (gt)
=.>AD/DB= AE/EB (h chat dg pg trong tam giac) (1)
Vi DF la dg pg cua goc ADC (gt)
=>FC/FA=ĐC/ĐÁ ( tính chất đg pg trong tam giác) (2)
tu (1) va (2) suy ra:EA/EB.FC/FA.DB.DC=AD/DB.DB/DC.DC/DA=1 (dpcm)

a: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng vơi ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC
b: \(AB=\sqrt{9\cdot25}=15\left(cm\right);AC=\sqrt{16\cdot25}=20\left(cm\right)\)
BE là phân giác
=>AE/AB=EC/CB
=>AE/3=CE/5=20/8=2,5
=>AE=7,5cm; CE=12,5cm
c: BM/MA*AE/EC*CN/BN
=BE/EA*AE/EC*EC/EB
=1
câu d dùng tính chất đường phân giác trong tam giác là ra mà em!
EM là phân giác của tam giác ABE=>BM/AM=BE/AE
EN là phân giác của tam giác BEC =>CN/BN=EC/BE
=> BM/AM * CN/BN*AE/EC= BE/AE * EC/BE*AE/EC=1