Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

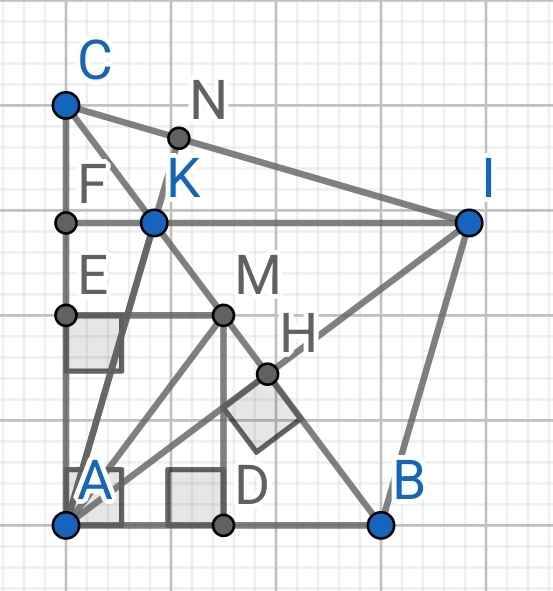
a) Tứ giác ADME có:
∠AEM = ∠ADM = ∠EAD = 90⁰ (gt)
⇒ ADME là hình chữ nhật
b) Do HI = HA (gt)
⇒ H là trung điểm của AI
Do HK = HB (gt)
⇒ H là trung điểm của BK
Tứ giác ABIK có:
H là trung điểm của AI (cmt)
H là trung điểm của BK (cmt)
⇒ ABIK là hình bình hành
⇒ IK // AB
Mà AB ⊥ AC (∆ABC vuông tại A)
⇒ IK ⊥ AC
⇒ IK là đường cao của ∆ACI
Lại có:
AH ⊥ BC (do AH là đường cao của ∆ABC)
⇒ CH ⊥ AI
⇒ CH là đường cao thứ hai của ∆ACI
∆ACI có:
IK là đường cao (cmt)
CH là đường cao (cmt)
⇒ AK là đường cao thứ ba của ∆ACI
⇒ AK ⊥ IC

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
b: Xét tứ giác ABKI có
M là trung điểm chung của AK và BI
Do đó: ABKI là hình bình hành
=>KI//AB
mà AB\(\perp\)AC
nên KI\(\perp\)AC
Xét ΔCAI có
IK,CH là đường cao
IK cắt CH tại K
Do đó: K là trực tâm của ΔCAI
=>AK\(\perp\)IC

a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
\(\widehat{BAC}=90^0\)
Do đó: ABDC là hình chữ nhật
b: Xét ΔADE có
M,H lần lượt là trung điểm của AD,AE
=>MH là đường trung bình
=>MH//DE
=>DE vuông góc AE
Xét tứ giác ABED có \(\widehat{ABD}=\widehat{AED}=90^0\)
=>ABED là tứ giác nội tiếp
=>\(\widehat{BDE}=\widehat{EAB}\)
=>\(\widehat{BDE}=\widehat{HAB}=\widehat{C}\)
=>\(\widehat{BDE}=\widehat{C}\)
mà \(\widehat{ACB}=\widehat{ADB}\)
nên \(\widehat{BDE}=\widehat{ADB}\)
=>DB là phân giác của \(\widehat{ADE}\)

b: Xét tứ giác ABDK có
H là trung điểm chung của AD và BK
AD vuông góc BK tại H
Do đó: ABDK là hình thoi
=>AK//BD
c: ABDK là hình thoi
=>AB=BD

Hình tự vẽ nha :
a)
Ta có : HI \(\perp\)AB => AI \(\perp\)IH
<=> AI là đường cao của tam giác AEH
Mà : EI = IH ( gt )
=> tam giác AEH cân tại A
=> AE = AH
b) chứng minh tương tự như câu (a)

a, Xét ∆AHC và ∆DHC có:
+CH chung
+\(\widehat{CHA}=\widehat{CHD}\left(=90^o\right)\)
+HA=HC(gt)
\(\Rightarrow\)∆HCA=∆HCD(ch-cgv)
A B C H D E K
a/ Xét tg vuông AHC và tg vuông DHC có
HC chung
HA = HD (gt)
=> tg AHC = tg DHC (Hai tg vuông có 2 cạnh góc vuông bằng nhau)
b/ K là giao của AE và CD
Xét tg vuông ABC có
\(\widehat{BAH}=\widehat{ACB}\) (cùng phụ với góc \(\widehat{ABC}\) ) (1)
tg AHC = tg DHC (cmt) => \(\widehat{DCH}=\widehat{ACB}\) (2)
Xét tg vuông ABH và tg vuông AEH có
AH chung; HB = HE (gt) => tg ABH = tg AEH (hai tg vuông có 2 cạnh góc vuông bằng nhau) \(\Rightarrow\widehat{BAH}=\widehat{EAH}\) (3)
Từ (1) (2) (3) => \(\widehat{EAH}=\widehat{DCH}\) (4)
Xét tg vuông AHE có
\(\widehat{EAH}+\widehat{AEH}=90^o\) (5)
Mà \(\widehat{AEH}=\widehat{CEK}\) (góc đối đỉnh) (6)
Từ (4) (5) (6) \(\Rightarrow\widehat{DCH}+\widehat{CEK}=90^o\Rightarrow\widehat{AKC}=90^o\)
\(\Rightarrow AK\perp CD\) mà \(CH\perp AD\) => E là trực tâm của tg ADC
c/
tg ABH = tg AEH (cmt) => AB = AE
tg AHC = tg DHC (cmt) => AC = CD
Xét tg ABC có
\(AB+AC>BC\) (trong tg tổng độ dài 2 cạnh lớn hớn độ dài cạnh còn lại)
\(\Rightarrow AE+CD>BC\)