Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, HA^2=HB.HC
Xet tg AHB va tg AHC
Có: H chung
Va góc HCA= góc ABH ( phụ với Â)
=>Tam giác AHB đồng dạng tam giác AHC
=> AH/BH=HC/AH
=>đpcm
b, Ta có: AH/BH=HC/AH
=>AH^2=BH.HC
=>AH^2=144
=>AH=12
*Tính AC
Áp dụng định lý Pi-ta-go:
AC^2=AH^2+HC^2
AC^2=144+256
AC=20cm
*Tính AB
Áp dụng định lý Pi-ta-go:
AB^2=BH^2+AH^2
AB^2=81+144
AB^2=225
AB=15cm

3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)

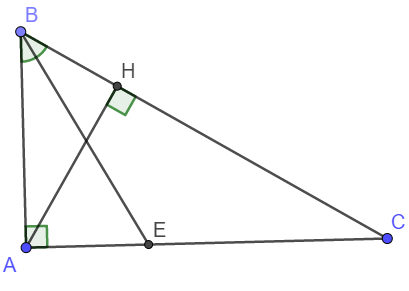
a) Xét tam giác ABC và tam giác HBA có:
\(\widehat{BAC}=\widehat{BHA}=90^o\)
Góc B chung
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right)\)
b)
Xét tam giác ABC và tam giác HAC có:
\(\widehat{BAC}=\widehat{AHC}=90^o\)
Góc C chung
\(\Rightarrow\Delta ABC\sim\Delta HAC\left(g-g\right)\)
c) Từ câu a và b ta có : \(\Delta HBA\sim\Delta HAC\)
\(\Rightarrow\frac{HB}{HA}=\frac{HA}{HC}\Rightarrow HA^2=HB.HC=9.16=144\)
\(\Rightarrow HA=12\left(cm\right)\)
Khi đó áp dụng định lý Pi-ta-go ta có:
\(AB^2=BH^2+AH^2=9^2+12^2\Rightarrow AB=15\left(cm\right)\)
\(AC^2=CH^2+AH^2=16^2+12^2\Rightarrow AC=20\left(cm\right)\)
BC = BH + HC = 9 + 16 = 25 (cm)
Áp dụng tính chất tia phân giác trong tam giác ta có:
\(\frac{AE}{EC}=\frac{AB}{BC}=\frac{15}{25}=\frac{3}{5}\)
\(\Rightarrow AE=\frac{3}{8}\times20=7,5\left(cm\right)\)
\(\Rightarrow EC=20-7,5=12,5\left(cm\right)\)

Lời giải:
a)
Xét tam giác $BHA$ và $AHC$ có:
\(\widehat{BHA}=\widehat{AHC}=90^0\)
\(\widehat{HBA}=\widehat{HAC}(=90^0-\widehat{BAH})\)
\(\Rightarrow \triangle BHA\sim \triangle AHC(g.g)\Rightarrow \frac{BH}{AH}=\frac{HA}{HC}\)
\(\Rightarrow AH^2=BH.CH\)
Ta có đpcm.
b)
Từ kết quả phần a suy ra \(AH^2=HB.HC=9.16\Rightarrow AH=12\) (cm)
Áp dụng định lý Pitago cho tam giác vuông $AHB, AHC$:
\(BA=\sqrt{HA^2+BH^2}=\sqrt{12^2+9^2}=15\) (cm)
\(CA=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20\) (cm)
\(BC=HB+HC=9+16=25\) (cm)

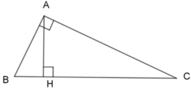
Với BH = 9cm, HC = 16cm => BC = BH + HC = 9 + 16 = 25 cm
Ta có: A H 2 = HB.HC (cmt)
=> A H 2 = 9.16 = 144 => AH = 12cm
Nên diện tích tam giác ABC là S A B C = 1 2 .AH.BC = 1 2 .12.25 = 150 c m 2
Đáp án: C



a) Xét \(\Delta HAC\)và \(\Delta HBA\) có:
\(\widehat{AHC}=\widehat{BHA}=90^0\)
\(\widehat{HAC}=\widehat{HBA}\) cùng phụ với \(\widehat{HAB}\)
suy ra: \(\Delta HAC~\Delta HBA\)
\(\Rightarrow\)\(\frac{AH}{HB}=\frac{HC}{AH}\)
\(\Rightarrow\)\(AH^2=HB.HC\)