Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với bài toán này, ta sử dụng hệ thức lượng trong tam giác.
A B C H E F
a. Kiểm tra thấy \(AB^2+AC^2=BC^2\) nên tam giác ABC vuông tại A.
\(AH=\frac{AB.AC}{BC}=\frac{60}{13}\)
b. Áp dụng hệ thức lượng, ta thấy \(AB.EA=AH^2=AF.AC\)
c. Từ kết quả câu b và góc A vuông ta suy ra được \(\Delta AEF\sim\Delta ACB\left(c-g-c\right)\).

- Ap dung dinh ly pitago dao vao tam giac ABC ta co AB2+AC2=52+122=169=132 . ma BC2=132
- =>AB2+AC2=BC2=>Tam giac ABC vuong tai A
- Ke duong cao AH .Ap dung ti so luong giac vao tam giac vuong ABC ta co \(\frac{1}{AH^2}\)= \(\frac{1}{AB^2}\)+ \(\frac{1}{AC^2}\)=>\(\frac{1}{AH^2}\)= \(\frac{1}{5^2}\)+ \(\frac{1}{12^2}\)=>AH=\(\frac{60}{13}\)
3.Tu HE vuong goc voi AB , HF vuong goc voi AC =>HEA =900 , HFA =900 va BAC =900=>tu giac EHFA la hinh chu nhat =>goc AEF=EAH ma EAH=ACH vi cung phu voi goc HAC =>Ta chung minh duoc EAF ~ ABC 2.=>\(\frac{AB}{AF}\)= \(\frac{AC}{AE}\)=>AB\(\times\)AE = AF\(\times\)AC

Xét ΔABH vuông tại H(gt)
=> \(AH^2=AE\cdot AB\) (1)
Xét ΔAHC vuông tại C(gt)
=>\(AH^2=AF\cdot AC\) (2)
Từ (1)(2) suy ra:
AE.AB=AF.AC
b) Xét ΔABH vuông tại H(gt)
=> \(AB^2=AH^2+BH^2=3^2+4^2=9+16=25\)
=>AB=25
Áp dụng hệ thức ta có:
\(AH^2=AE\cdot AB\)
=> \(AE=\frac{AH^2}{AB}=\frac{4^2}{5}=\frac{16}{5}\)
Có: AB=AE+BE
=>BE=AB-AE= \(5-\frac{16}{5}=\frac{9}{5}\)

a: BC=BH+CH
=4+6
=10(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{4\cdot6}=2\sqrt{6}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{4\cdot10}=2\sqrt{10}\left(cm\right)\\AC=\sqrt{6\cdot10}=2\sqrt{15}\left(cm\right)\end{matrix}\right.\)
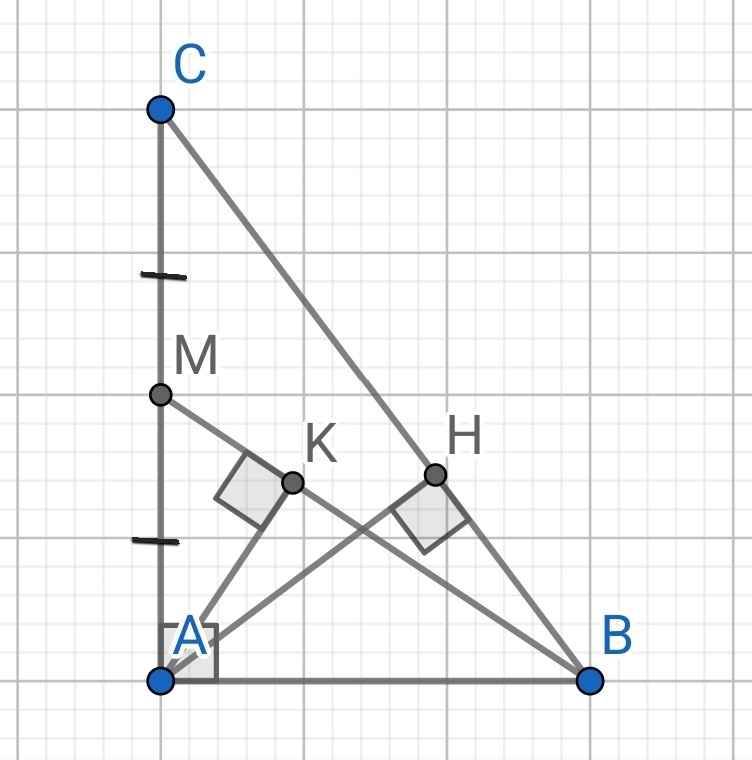
b: M là trung điểm của AC
=>\(AM=\dfrac{AC}{2}=\sqrt{15}\left(cm\right)\)
Xét ΔAMB vuông tại A có
\(tanAMB=\dfrac{AB}{AM}=\sqrt{\dfrac{2}{3}}\)
=>\(\widehat{AMB}\simeq39^0\)
c: ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\left(2\right)\)
Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)

b: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)