Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình hơi xấu bạn nhé
ta có góc C = 30 độ nên
=> góc B = 60 độ (1)
ta lại có BM= BA
=> tam giác ABM là ta giác cân tại B (2)
từ (1) và (2) => tam giác ABM lả tam giác đều
b, ta có thể chứng minh tam giác AMC cân tại M ( vì có 2 góc kề đấy = nhau và = 30 độ )
=> MC = AM ( 1)
theo câu a ta có
ABM là tam giác đều nên AM = BM ( 2)
từ (1)và (2)
=> BM = MC mà BM + MC= BC
=> AM = BM = BC/2

ok, thanks nhưng dừng khoảng chừng là 2 giây, you lấy từ qanda

a/ Xét t/g ABM vg tại A và t/g DBM vg tại D có
BM : chung
\(\widehat{ABM}=\widehat{CBM}\)
=> t/g ABM = t/g DBM
=> AB = BD
Mà \(\widehat{ABC}+\widehat{C}=90^O\) => \(\widehat{ABC}=60^o\)
=> t/g ABD đều
b/ t/g ABM = t/g DBM
=> AM = DM ; \(\widehat{BDM}=\widehat{BAC}=90^o\)
Suy ra t/g CMD vg tại D
=> MC > DM
=> MC > AM
c/ Xét t/g MAE vg tại A và t/g MDC vg tại D có
AM = MD
AE = DC
=> t/g MAE = t/g MDC
=> \(\widehat{AME}=\widehat{DMC}\)
Mà 2 góc này đối đỉnh
=> D,M,E thẳng hàng
a) Xét ΔABM vuông tại A và ΔDBM vuông tại D có
BM chung
\(\widehat{ABM}=\widehat{DBM}\)(BM là tia phân giác của \(\widehat{ABD}\))
Do đó: ΔABM=ΔDBM(cạnh huyền-góc nhọn)
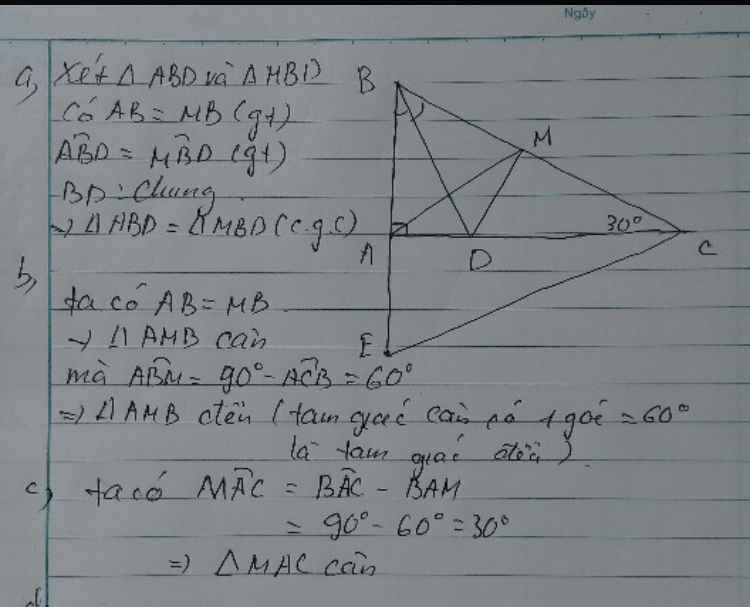
Giúp em mk đi mk