Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC vuông tại A có \(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-30^0=60^0\)
Xét ΔBAM có BA=BM và \(\widehat{ABM}=60^0\)
nên ΔBAM đều
b: Ta có: ΔMAB đều
=>\(\widehat{MAB}=60^0\)
Ta có: \(\widehat{MAB}+\widehat{MAC}=\widehat{BAC}\)
=>\(\widehat{MAC}+60^0=90^0\)
=>\(\widehat{MAC}=30^0\)
Xét ΔMAC có \(\widehat{MAC}=\widehat{MCA}\left(=30^0\right)\)
nên ΔMAC cân tại M
=>MA=MC
mà MB=MA
nên MB=MC
=>M là trung điểm của BC
=>\(AM=MB=\dfrac{1}{2}BC\)
c: Ta có: ΔMAC cân tại M
mà MD là đường phân giác
nên MD\(\perp\)AC
Ta có: MD\(\perp\)AC
AB\(\perp\)AC
Do đó: MD//AB

(Bạn tự vẽ hình giùm)
a/ Ta có BA = BD (gt)
nên \(\Delta BAD\)cân tại B
=> \(\widehat{BAD}=\frac{180^o-\widehat{B}}{2}\)
=> \(\widehat{BAD}=\frac{180^o-60^o}{2}\)
=> \(\widehat{BAD}=\widehat{BDA}=60^o=\widehat{B}\)
=> \(\Delta BAD\)đều (đpcm)
b/ \(\Delta ABI\)và \(\Delta DBI\)có: AB = DB (gt)
\(\widehat{ABI}=\widehat{IBD}\)(BI là tia phân giác \(\widehat{B}\))
Cạnh BI chung
=> \(\Delta ABI\)= \(\Delta DBI\)(c. g. c) => \(\widehat{A}=\widehat{BDI}=90^o\)(hai cạnh tương ứng)
và AI = DI (hai cạnh tương ứng)
=> BI = IC (quan hệ giữa đường xiên và hình chiếu)
nên \(\Delta BIC\)cân tại I (đpcm)
c/ Ta có \(\Delta BIC\)cân tại I (cmt)
=> Đường cao ID cũng là đường trung tuyến của \(\Delta BIC\)
=> D là trung điểm BC (đpcm)
d/ Ta có \(\Delta ABC\)vuông tại A
=> BC2 = AB2 + AC2 (định lý Pythagore)
=> AB2 + AC2 = 262 = 676
và \(\frac{AB}{AC}=\frac{5}{2}\)=> \(\frac{AB}{5}=\frac{AC}{2}\)=> \(\frac{AB^2}{25}=\frac{AC^2}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{AB^2}{25}=\frac{AC^2}{4}=\frac{AB^2+AC^2}{25+4}=\frac{676}{29}\)
=> \(\hept{\begin{cases}\frac{AB}{5}=\frac{676}{29}\\\frac{AC}{2}=\frac{676}{29}\end{cases}}\)=> \(\hept{\begin{cases}AB=\frac{676}{29}.5\\AC=\frac{676}{29}.2\end{cases}}\)=> \(\hept{\begin{cases}AB=\frac{3380}{29}\left(cm\right)\\AC=\frac{1352}{29}\left(cm\right)\end{cases}}\)

ok, thanks nhưng dừng khoảng chừng là 2 giây, you lấy từ qanda

Bạn tự vẽ hình nhé!
\(\Delta BDA=\Delta BDM\left(c.g.c\right)\)vì BA = BM (gt) ;\(\widehat{ABD}=\widehat{MBD}\)(BD là phân giác góc B : gt) ; chung BD
\(\Rightarrow\widehat{A}=\widehat{DMB}\)(2 góc tương ứng) mà\(\widehat{A}\)= 900 (\(\Delta ABC\)vuông tại A : gt)\(\Rightarrow\widehat{DMB}=90^0\)=> DM vuông góc BC
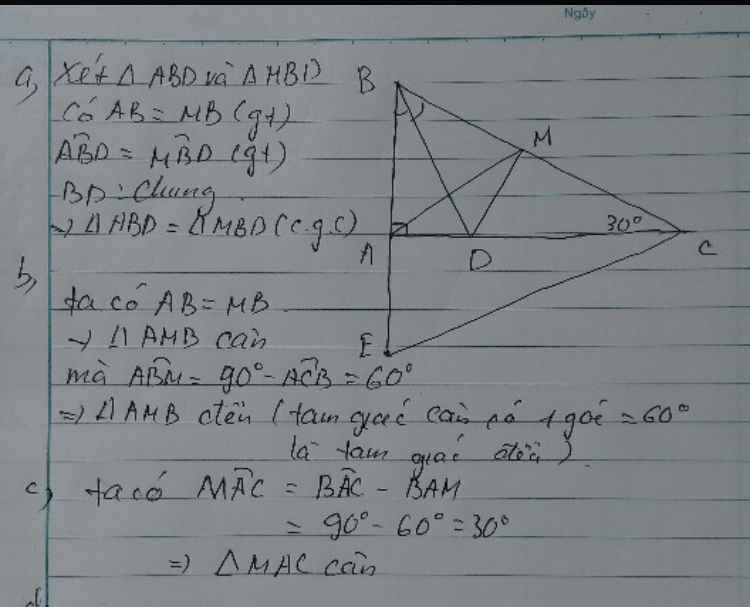
hình hơi xấu bạn nhé
ta có góc C = 30 độ nên
=> góc B = 60 độ (1)
ta lại có BM= BA
=> tam giác ABM là ta giác cân tại B (2)
từ (1) và (2) => tam giác ABM lả tam giác đều
b, ta có thể chứng minh tam giác AMC cân tại M ( vì có 2 góc kề đấy = nhau và = 30 độ )
=> MC = AM ( 1)
theo câu a ta có
ABM là tam giác đều nên AM = BM ( 2)
từ (1)và (2)
=> BM = MC mà BM + MC= BC
=> AM = BM = BC/2