Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét Tam giác HBA và Tam giác ABC có
B Chung
Góc H=A(=90 độ)
=> tam giác HBA Đồng dạng với tam giác giác ABC (g.g)
=> AH/AC=AB/BC
(BC)^2=AB^2+AC^2
BC^2=400
BC=20
AH/AC=AB/BC => AH=AB.AC/BC=16x12/20=9.6

Tự vẽ hình nha
a) xét tam giác HAB và tam giác ABC
góc AHB = góc ABC
góc CAB : chung
Suy ra : tam giác AHB ~ tam giác ABC ( g-g )
b) Áp dụng định lí py - ta - go vào tam giác ABC ta được :
AC2 + AB2 = BC2
162 + 122 = BC2
400 = BC2
=> BC = \sqrt{400}400= 20 ( cm )
ta có tam giác HAB ~ tam giác ABC ( câu a )
=> \frac{AH}{AC}=\frac{AB}{BC}hay\frac{AH}{16}=\frac{12}{20}ACAH=BCABhay16AH=2012
=> AH = \frac{12.16}{20}=9,62012.16=9,6( cm )
Độ dài cạnh BH là
Áp dụng định lí py - ta - go vào tam giác HBA ta được :
AH2 + BH2 = AB2
BH2 = AB2 - AH2
BH2 = 122 - 9,62
BH2 = 51,84
=> BH = \sqrt{51,84}51,84 = 7,2 ( cm )
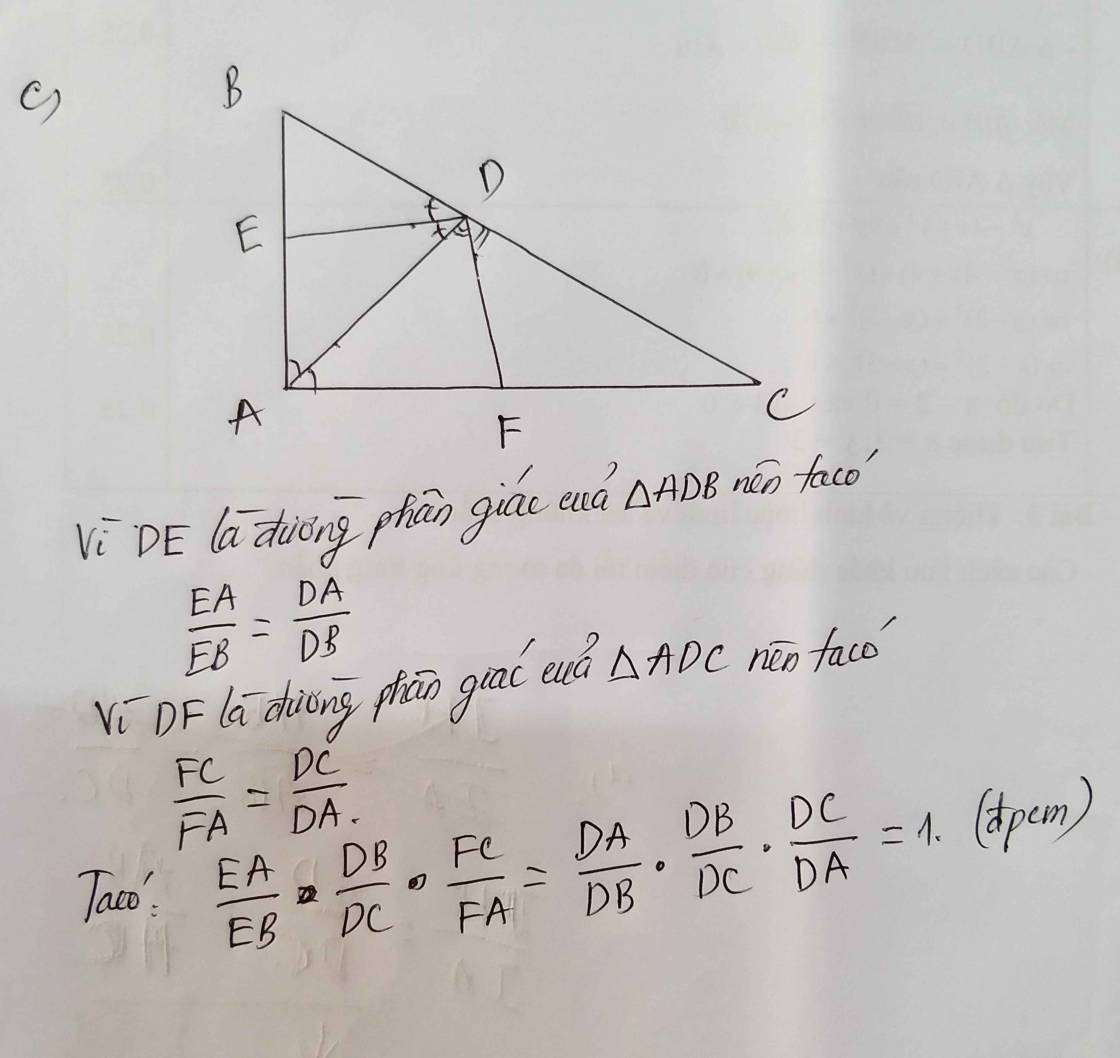
c) Vì AD là đường phân giác của tam giác ABC nên :
\frac{AB}{BD}=\frac{AC}{CD}\Leftrightarrow\frac{AB}{BC-CD}=\frac{AC}{CD}BDAB=CDAC⇔BC−CDAB=CDAC
<=> \frac{AB.CD}{CD\left(BC-CD\right)}=\frac{AC\left(BC-CD\right)}{CD\left(BC-CD\right)}CD(BC−CD)AB.CD=CD(BC−CD)AC(BC−CD)
<=> AB.CD = AC(BC - CD)
hay 12CD = 16.20 - 16CD
<=> 12CD+ 16CD = 320
<=> 28CD = 320
<=> CD = \frac{320}{28}\approx11.43\left(cm\right)28320≈11.43(cm)
Độ dài cạnh BD là :
BD = BC - CD
BD = 20 - \frac{320}{28}28320\approx≈ 8,57 ( cm )

xét Tam giác HBA và Tam giác ABC có
B Chung
Góc H=A(=90 độ)
=> tam giác HBA Đồng dạng với tam giác giác ABC (g.g)
=> AH/AC=AB/BC
(BC)^2=AB^2+AC^2
BC^2=400
BC=20
AH/AC=AB/BC => AH=AB.AC/BC=16x12/20=9.6

AMAM là đường trung tuyến ứng với cạnh huyền nên AM=BC2=BMAM=BC2=BM
⇒△MAB⇒△MAB cân tại MM
⇒BAMˆ=MBAˆ⇒BAM^=MBA^
Ta có:
BADˆ=DAMˆ−BAMˆ=900−MBAˆ=900−HBAˆBAD^=DAM^−BAM^=900−MBA^=900−HBA^
HABˆ=900−HBAˆHAB^=900−HBA^
⇒BADˆ=HABˆ⇒BAD^=HAB^ nên ABAB là tia phân giác DAHˆDAH^ (đpcm)
b)
Xét tam giác CADCAD và ABDABD có:
DˆD^ chung
ACDˆ=900−ABHˆ=BADˆACD^=900−ABH^=BAD^
⇒△CAD∼△ABD⇒△CAD∼△ABD (g.g)
⇒CAAB=ADBD=CDAD⇒CAAB=ADBD=CDAD
⇒CA2AB2=CDBD(∗)⇒CA2AB2=CDBD(∗)
Dễ thấy △BAH∼△BCA△BAH∼△BCA (g.g) và △CAH∼△CBA△CAH∼△CBA (g.g)
⇒BABC=BHBA⇒BABC=BHBA và CACB=CHCACACB=CHCA
⇒AB2=BC.BH⇒AB2=BC.BH và AC2=CH.BCAC2=CH.BC
⇒AC2AB2=CHBH(∗∗)⇒AC2AB2=CHBH(∗∗)
Từ (∗);(∗∗)⇒CDBD=CHBH(∗);(∗∗)⇒CDBD=CHBH
⇒CD.BH=CH.BD⇒CD.BH=CH.BD (đpcm)
Hình bạn tự vẽ nhé...
a)
Xét tam giác BAH và tam giác ABC , có :
A^ = H^ = 90O
B^ : góc chung
=> tam giác HAB ~ tam giác ACB ( g.g)
c)
ADĐL pitago vào tam giác vuông ABC , có :
AB2 + AC2 = BC2
=> 122 + 166 = BC2
=> BC2 = 400
=> BC = 20 cm
Vì tam giác ACB ~ tam giác HAB , nên ta có :
AH/AC= AB/BC
=> AH/16=12/20
=> AH = 9,6 cm.