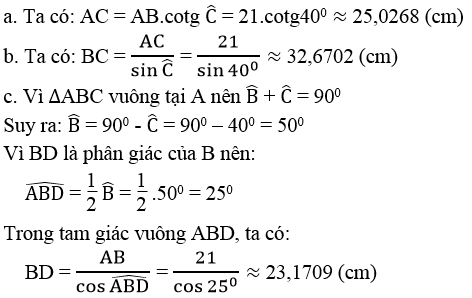Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Ta có: SinC = \(\frac{AB}{BC}\)=> Sin40 = \(\frac{10}{BC}\)=> BC = 15.5 (cm)
b) Có B = 90 độ - 40 độ = 60 độ
=> Góc ABD = 60/2 = 30 độ
Ta có TanABD = \(\frac{AD}{BA}\)=> Tan30 = \(\frac{AD}{10}\)=> AD = \(\frac{\sqrt{3}\cdot10}{3}\)

Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{C}+\widehat{ABC}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{ABC}=50^0\)
\(\Leftrightarrow\widehat{ABD}=25^0\)
Xét ΔABD vuông tại A có
\(AB=BD\cdot\cos\widehat{ABD}\)
\(\Leftrightarrow BD=\dfrac{21}{\cos25^0}\simeq23.2\left(cm\right)\)

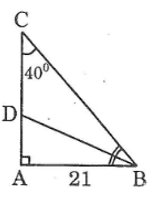
a) Ta có: \(AC=AB.\cot\widehat{C}=21.\cot\widehat{40^o}\simeq25,0268\left(cm\right)\)
b) Ta có: \(BC=\dfrac{AC}{\sin\widehat{C}}=\dfrac{21}{\sin\widehat{40^o}}\simeq32,6702\left(cm\right)\)
c) Vì ΔABCΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
Suy ra: \(\widehat{B}=90^o-\widehat{C}=90^o-40^o=50^o\)
Vì BD là phân giác của B nên:
\(\widehat{ABD}=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}.50^o=25^o\)
Trong tam giác vuông ABD, ta có:
\(BD=\dfrac{AB}{\cos\widehat{ABD}}=\dfrac{21}{\cos25^o}\simeq23,1709\left(cm\right)\)

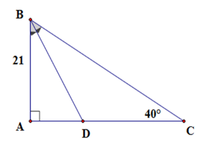
Xét tam giác ABC vuông tại A có A B C ^ + C ^ = 90 o ⇒ A B C ^ = 50 o
Mà BD là phân giác góc ABC nên A B D ^ = 1 2 A B C ^ = 25 0
Xét tam giác ABD vuông tại A ta có B D = A B c o s A B D ^ = 21 c o s 25 o ≈ 23 , 2 c m
Đáp án cần chọn là: D