Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

NA/BA = NC/BC
Vì Tam giác ABC vuông tại A, biết AB=3cm,BC=5cm => AC= 4(cm)
=> NC-NA=4 (cm)
=> NC/BC = NA/BA = ( NC-NA)/(BC-AB) = 2
=> NA= BA*2 =6 (cm)

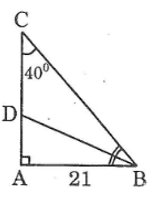
a) Ta có: \(AC=AB.\cot\widehat{C}=21.\cot\widehat{40^o}\simeq25,0268\left(cm\right)\)
b) Ta có: \(BC=\dfrac{AC}{\sin\widehat{C}}=\dfrac{21}{\sin\widehat{40^o}}\simeq32,6702\left(cm\right)\)
c) Vì ΔABCΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
Suy ra: \(\widehat{B}=90^o-\widehat{C}=90^o-40^o=50^o\)
Vì BD là phân giác của B nên:
\(\widehat{ABD}=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}.50^o=25^o\)
Trong tam giác vuông ABD, ta có:
\(BD=\dfrac{AB}{\cos\widehat{ABD}}=\dfrac{21}{\cos25^o}\simeq23,1709\left(cm\right)\)

Tham khảo tại đây nha:
Câu hỏi của Moe - Toán lớp 9 - Học toán với online math
mã câu :1308090

xét tg ABCD có \(\widehat{A}+\widehat{C}=180^0\)
\(\Rightarrow\)ABCD là tg nt (O) ( tg có tổng 2 góc đối = 1800 là tg nt )
xét (O) có \(\widehat{DAC}=\widehat{BAC}\)( AC là tia pg của \(\widehat{DAC}\))
\(\Rightarrow\)\(\widebat{DC}=\widebat{BC}\)(2 góc nt = nhau chắn 2 cung = nhau)
\(\Rightarrow\widehat{DBC}=\widehat{BDC}\)( 2 CUNG = NHAU CHẮN 2 GÓC NT = NHAU)
\(\Rightarrow\)\(\Delta BDC\)cân tại C
mà CK là đường trung tuyến của \(\Delta BDC\)(K là trung điểm của BD)
\(\Rightarrow\)CK đồng thời là đường cao , đường trung tuyến , tia pg của \(\Delta BDC\)
\(\Rightarrow\)\(CK\perp BD\) (1)
xét \(\Delta BDE\)là tam giác đều có CK là đường trung tuyến ( k là trung điểm của BD)
\(\Rightarrow\)EK đồng thời là đường cao , trung tuyến và tia phân giác của \(\Delta BDE\)
\(\Rightarrow EK\perp BD\) (2)
TỪ (1) VÀ (2) \(\Rightarrow\)E , C , K thẳng hàng
#mã mã#

Câu c)
Ta có: AD là phân giác ^BAC
=> ^BAD = ^ DAC = ^BAC : 2 = 90o : 2 = 45o
Xét \(\Delta\)AIB có: ^AIB = 90o; ^BAI = ^BAD = 45o
=> ^ABI = 45o
Xét \(\Delta\)BAM vuông tại A có: ^ABM = ^ABI = 45o => ^AMB = 45o => \(\Delta\)ABM vuông cân
có AI là đường cao => AI là đường trung tuyến => I là trung điểm BM
=> BM = 2 BI
Xét \(\Delta\)ABM vuông tại A có AI là đương cao => AB2 = BI.BM = BI.2BI = 2BI2
Xét \(\Delta\)ABC vuông tại A có: AH là đường cao: => AB2 = BH.BC
=> BH.BC = 2BI2
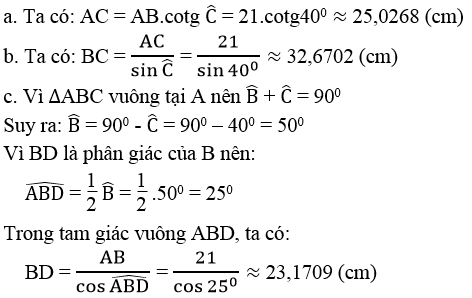
Xét tam giác ABC vuông tại A có A B C ^ + C ^ = 90 o ⇒ A B C ^ = 50 o
Mà BD là phân giác góc ABC nên A B D ^ = 1 2 A B C ^ = 25 0
Xét tam giác ABD vuông tại A ta có B D = A B c o s A B D ^ = 21 c o s 25 o ≈ 23 , 2 c m
Đáp án cần chọn là: D